Vgbhfive's Blog

数据结构-基数树

Posted on

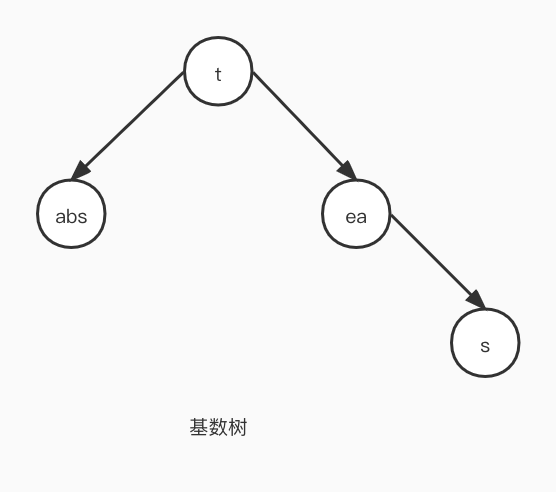
定义

基数树在计算机科学中，被翻译为 Radix Tree 或者 Compact Prefix Tree，是一种用于进行空间存储优化的数据结构，其最大的区别点在于它不是按照每个字符长度作为节点进行拆分，而是将一个或多个字符作为一个分支来存储数据，这可以避免长字符出现很深的节点。
neo4j-10.jpeg

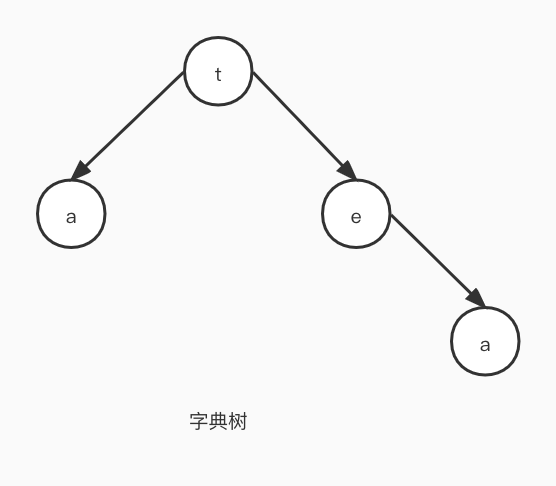
与此相关的有字典树，字典树的原理是将每个字符按照长度进行拆分，然后对应到每一个分支上去，分支所在的末节点对应从根节点到当前节点拼接出来的字符串就是存储的数据。
neo4j-11.jpeg

使用场景

元素个数不是太多，但是元素之间通常有很长的相同前缀时很适合采用 Radix Tree 来存储。

示例：

  • 在构建 IP 路由应用方面 Radix Tree 很广泛，因为 IP 通常具有大量相同的前缀。
  • 在倒排索引方面 Radix Tree 也使用广泛。
  • 另外在模式匹配方面也有其独到的使用。

Radix Tree 操作

Radix Tree 支持新增、搜索、删除等操作。新增操作是新增一个新的字符串到基数树中并尝试最小化数据存储（即对某些节点进行合并）。删除操作就是从基数树中移除一个字符串。而搜索操作包含严格查找、前缀查找、后缀查找已经查询某个前缀的所有字符串。所有的这些操作的时间复杂度都是 O(k （其中 k 是字符串集合中最长的字符串长度）。

下面的实现逻辑与标准实现逻辑不太一致，参考其思路即可。

基础信息

目前这里的需求为构建模型，然后去匹配对应的路径是否存在于模型中即可。

1
2
3
4
5
6
7
8
9
10
class Node {
	String node;
	boolean isEnd = false;
	HashMap<String, Node> maps;	

	public Node(String node, HashMap<String, TreeNode> maps) {
	    this.node = node;
	    this.maps = maps;
	}
}

查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public boolean match(String x) {
    TreeNode node = this;
    String[] matches = x.split("\\.");
    if (!this.node.equals(matches[0])) {
        return false;
    }
    for (int i = 1; i < matches.length; i++) {
        node = node.matchNode(matches[i]);
        if (node == null) {
            return false;
        }
    }
    return true && node.isEnd;
}

新增

1
2
3
4
5
6
7
8
9
10
11
12
13
public void add(String[] params) {
    TreeNode node = this;
    for (String param : params) {
        node.addNode(param);
    }
}
public void addNode(String x) {
    TreeNode node = this;
    for (String s : x.split("\\.")) { // 这里以 . 作为父子节点的区分
        node = node.addTreeNode(s);
    }
    node.isEnd = true;
}

合并

1
2
3
4
5
6
7
8
9
public void merge(TreeNode node) {
    StringBuilder builder = new StringBuilder();
    DFSToString(node, "", builder, "\n");
    String[] strings = builder.toString().split("\n");
    for (int i = 0; i < strings.length; i++) {
        strings[i] = strings[i].substring(1);
    }
    this.add(strings);
}

其他

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
private String BFSToString(TreeNode node) {
    StringBuilder builder = new StringBuilder();
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(node);
    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode tmp = queue.poll();
            if (i == (size - 1)) {
                builder.append(tmp.node);
            } else {
                builder.append(tmp.node + " - ");
            }
            for (Map.Entry<String, TreeNode> map : tmp.maps.entrySet()) {
                queue.add(map.getValue());
            }
        }
        if (!queue.isEmpty()) builder.append("\n");
    }
    return builder.toString();
}

private void DFSToString(TreeNode node, String path, StringBuilder builder, String split) {
    if (node.maps.isEmpty()) {
        builder.append(path + "." + node.node + split);
    } else {
        for (Map.Entry entry : node.maps.entrySet()) {
            String key = (String) entry.getKey();
            TreeNode tmp = (TreeNode) entry.getValue();
            if (tmp.isEnd) {
                builder.append(path + "." + key + split);
                if (!tmp.maps.isEmpty()) {
                    DFSToString(tmp, path + "." + key, builder, split);
                }
            } else {
                DFSToString(tmp, path + "." + key, builder, split);
            }
        }
    }
}

public String RecordToString() {
    StringBuilder builder = new StringBuilder();
    DFSToString(this, this.node, builder, ",");
    StringBuilder ret = new StringBuilder();
    for (String s : builder.toString().split(",")) {
        ret.append(s.substring(SensitiveConstant.initName.length()+1)).append(",");
    }
    return ret.toString().substring(0, ret.length()-1);
}

看到这里貌似与基数树的思路不太一致，毕竟再好的数据结构也要与实际业务相挂钩，但是这里的思想与基数树是一致的。

测试与输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 模型输出
risk
a - b - c - d - e - f - g - h
ca - fa - da - fb
risk.a
risk.b
risk.c.ca
risk.d
risk.e
risk.f.fa
risk.f.da
risk.f.fb
risk.g
risk.h

// 模型匹配结果
key matched!

引用

个人备注

此博客内容均为作者学习所做笔记，侵删！
若转作其他用途，请注明来源！