Vgbhfive's Blog

ML-TabNet浅析

Posted on Edited on

简介

随着机器学习与深度学习的发展，DNN 在图像、语音和文本类型的数据上都有了广泛的应用，其优势如下：

  • 类似图像、文本，通过对其数据进行编码，从而得到一个表征表格数据。
  • 减少对特征工程的依赖（参加过 kaggle 竞赛的同学都知道特征在模型中的重要性）。
  • 可通过 online learning 的方式更新模型。

而在表格类数据的任务中，大部分都是由决策树模型成为标配，其优势如下：

  • 可以根据决策树回溯其推理过程，可解释性较强。
  • 决策树的流形可以看作是超平面的边界，对于表格类数据的效果很好。
  • 训练速度很快。

因此如果有一种模型即吸收决策树模型的可解释性和稀疏特征选择优点，也具有 DNN 的 end-to-end 长处，那毫无疑问就是针对表格数据的利器 - TabNet 。

整体架构

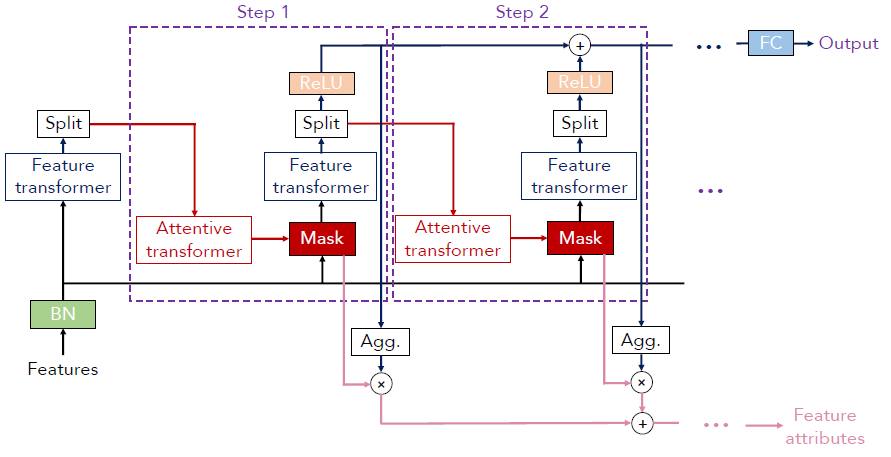
TabNet 整体架构如下图所示：

  • 特征首先通过 BatchNorm 层，才能作为其他阶段的输入。
  • 网络中存在重复的结构 Step，各个 Step 的输入均是 BN 层的输出。
  • Step 中包含两个最重要的组件 Feature transformer 与 Attentive trandformer，该两个组件均有 BN 层、FC 层组成，其内部的堆叠个数可作为超参数进行配置。
  • Feature transformer 特征处理，其输出经过一个分裂 Split 部分，一部分经由 ReLU 之后得到输出；另一部分作为 Attentive transformer 的输入。
  • Attentive transformer 权重系数特征选择，其输出得到 Mask 稀疏掩码矩阵。
  • 各个 Step 输出求和后，同时经过 FC 层变换映射得到模型的最终输出。
  • Mask 稀疏掩码矩阵输出累加之后构成 Feature attributes，其用于模型的可解释性。

all.jpg

具体模块

特征处理

特征处理组件 Feature transformer 其被设计成串行的方式，网络结构如下图所示：

  • Shared across decision steps 各个 Step 共享层，即在各个 Step 中都是被共享的。
  • Decision step dependent 各个 Step 独立层，即在每层需要单独训练。

1.jpg

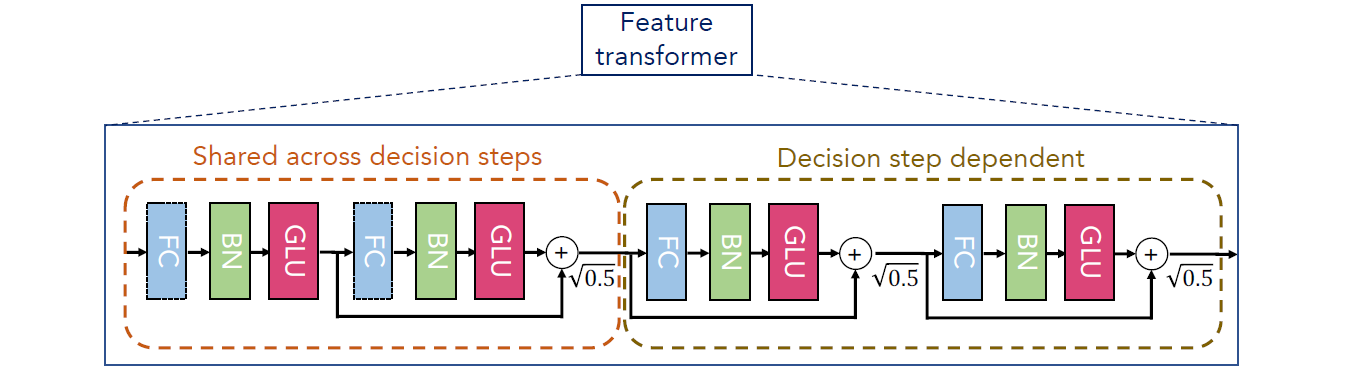
通过图中的网络结构可以将 FC、BN、GLU 看作一个 block。
其中 GLU(Gated Linear Unit) 是广义线性单元，其完成的变换如下：$GLU(a,b)=a \otimes \sigma (b)$，即输入两个相同 shape 的矩阵，b 矩阵经 $\sigma$ 变换后，与 a 矩阵中对应的元素相乘。GLU 层的源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class GLU_Layer(torch.nn.Module):
    def __init__(self, input_dim, output_dim, fc=None,
                 virtual_batch_size=128, momentum=0.02):
        super(GLU_Layer, self).__init__()

        self.output_dim = output_dim
        if fc:
            self.fc = fc
        else:
            self.fc = Linear(input_dim, 2*output_dim, bias=False)
        initialize_glu(self.fc, input_dim, 2*output_dim)

        self.bn = GBN(2*output_dim, virtual_batch_size=virtual_batch_size,
                      momentum=momentum)

    def forward(self, x):
        x = self.fc(x)
        x = self.bn(x)
        out = torch.mul(x[:, :self.output_dim], torch.sigmoid(x[:, self.output_dim:]))
        return out

各个 block 通过跳层连接 skip-connection 后，再乘以 $\sqrt{0.5}$，用于防止网络中输出的方差变换波动太大，影响学习的稳定性。

最后 Feature transformer 在完成计算后需要经过 Split 分裂成两部分，其分别是：

  • d[i]：表示第 i 个 Step 上用于最终的模型输出。输出维度为 $R^{B*N_d}$，B 为 BatchSize，$N_d$ 为输出维度，经过 ReLU 后，用于最终的模型输出。
  • a[i]：表示第 i 个 Step 上用于 Attentive transformer 的输入。输出维度为 $R^{B*N_a}$，用于 Attentive transformer 的输入。

特征选择

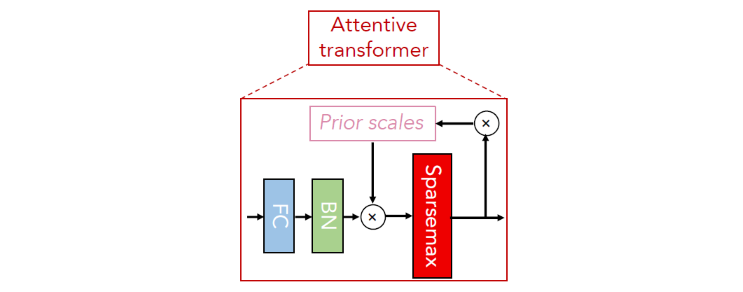
TabNet 的特征选择过程主要为每个 Step 学习一个 Mask 掩码矩阵，记为 $M[i] \in R^{B*D}$，其保持跟输入特征一样的 shape。其网络结构如下：

  • Mask 的计算公式：
    网络中存在一个加权缩放因子 Prior scales，记为 P，其 shape 与输入特征一致。
    当在 i 时刻，缩放因子与上一时刻 Feature transformer 的输出 a[i-1] 的关系为：
    $$ M[i] = sparemax(P[i-1] * h_i(a[i-1])) $$
    上式中的 sparemax 是归一化操作，类似于 softmax，不过其可以得到更稀疏的输出结果，即只选择最显著的特征，以此达到特征选择的目的。
    $h_i(a[i-1]))$ 指图中的 FC、BN 层。

  • 缩放因子的计算公式：
    $$ P[i] = _{j=1}^i (\gamma - M[j]) $$
    由上述公式可知，对于第 i 步中的缩放因子与 j=0,1...,i 步内的 Mask[j] 有关。
    公式中的 $\gamma$ 在不同的取值情况下会有不同的效果：

    • 当 $\gamma > 1$ 时，由于 M[j] 内的取值在 [0,1] 内且取值集中在 0 或 1 附近，特征在后续的 Step 中可以再次被以更高的权重使用。
    • 在 Step = 0 时刻 $P[0] = 1^{B * D}$，图中省略了该 Mask。

  • Mask 的稀疏性：
    为了保证 Mask 的稀疏性，需要对 M[i] 中要学习的参数进行正则化约束。其约束的方式为：对于网络中所有 Step 内涉及的 Mask 的参数 $M_{b,j}$，以如下公式求和作为损失函数的一部分：
    $$ L_{sparse} = sum_{i=i}^N sum_{b=1}^B sum_{j=1}^D {\frac {-M_{b,j}[i]} {N * B}} log(M_{b,j}[i] + \epsilon) $$

2.jpg

自监督学习

DNN 可以进行表征学习，而 TabNet 应用自监督学习，通过 encoder-decoder 框架来获得表格数据的 representation，从而也有助于分类和回归任务。如下图所示：

4.jpg

简单来说即认为同一样本之间不同特征是具有关联的，因此自监督学习则是先人为 Mask 一部分特征，然后通过 encoder-decoder 模型来对 Mask 的特征进行预测。
自监督学习的 encoder 部分如上图所示，而 decoder 部分如下所示：

5.jpg

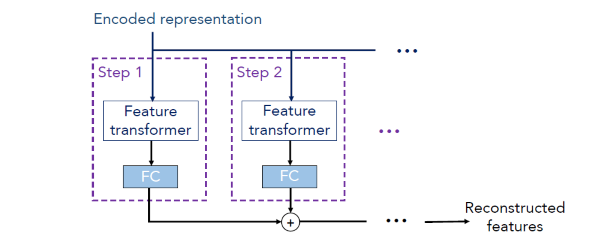
上面的 Encoded representation 就是 encoder 未经 FC 层的加和向量。
将其作为 decoder 的输入，decoder 同样利用 Feature transformer，其将 representation 向量重构为 Feature，之后经过若干个 Step 的加和，得到最后的重构 Feature。

最终输出

TabNet 的最终输出先对各个 Step 中 Feature transformer 的输出进行 ReLU 变换，最终对所有的 Step 中的输出进行求和，经过全连接层，得到最终的输出。即：

$$
\begin{equation}
\begin{split}
d_{out} = sum_{i=1}^N ReLU(d[i]) \\\\
output = FC(d_{out}) = W_{final} d_{out}
\end{split}
\nonumber
\end{equation}
$$

可解释性

结合 TabNet 的网络结构以及中间的组件 Feature transformer 和 Attentive transformer，从这些可以很明显的看出与 MLP 等神经网络的差异。MLP 神经网络中各层对输入特征均是无区别对待，而 TabNet 则是通过 Mask 矩阵来体现各个特征在不同 Step 中的重要性。

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
from pytorch_tabnet.tab_model import TabNetClassifier
from pytorch_tabnet.augmentations import ClassificationSMOTE
import torch
import scipy
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.preprocessing import LabelEncoder

# https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data
train = pd.read_csv('adult.csv')

# process data
nunique = train.nunique()
types = train.dtypes

categorical_columns = []
categorical_dims =  {}
for col in train.columns:
    if types[col] == 'object' or nunique[col] < 200:
        print(col, train[col].nunique())
        l_enc = LabelEncoder()
        train[col] = train[col].fillna("VV_likely")
        train[col] = l_enc.fit_transform(train[col].values)
        categorical_columns.append(col)
        categorical_dims[col] = len(l_enc.classes_)
    else:
        train.fillna(train.loc[train_indices, col].mean(), inplace=True)

target = ' <=50K'
train.loc[train[target]==0, target] = "wealthy"
train.loc[train[target]==1, target] = "not_wealthy"

# split data
X_train = train[features].values[train_indices]
y_train = train[target].values[train_indices]

X_valid = train[features].values[valid_indices]
y_valid = train[target].values[valid_indices]

X_test = train[features].values[test_indices]
y_test = train[target].values[test_indices]

# training model
tabnet_params = {"cat_idxs":cat_idxs,
                 "cat_dims":cat_dims,
                 "cat_emb_dim":2,
                 "optimizer_fn":torch.optim.Adam,
                 "optimizer_params":dict(lr=2e-2),
                 "scheduler_params":{"step_size":50, "gamma":0.9},
                 "scheduler_fn":torch.optim.lr_scheduler.StepLR,
                 "mask_type":'entmax', # "sparsemax"
                 "grouped_features" : grouped_features
                }
clf = TabNetClassifier(**tabnet_params)

aug = ClassificationSMOTE(p=0.2)
# This illustrates the behaviour of the model's fit method using Compressed Sparse Row matrices
sparse_X_train = scipy.sparse.csr_matrix(X_train)  # Create a CSR matrix from X_train
sparse_X_valid = scipy.sparse.csr_matrix(X_valid)  # Create a CSR matrix from X_valid
# Fitting the model
clf.fit(
    X_train=sparse_X_train, y_train=y_train,
    eval_set=[(sparse_X_train, y_train), (sparse_X_valid, y_valid)],
    eval_name=['train', 'valid'],
    eval_metric=['auc'],
    max_epochs=max_epochs, 
    patience=20,
    batch_size=1024, 
    virtual_batch_size=128,
    num_workers=0,
    weights=1,
    drop_last=False,
    augmentations=aug, #aug, None
)

# plot
# losses
plt.plot(clf.history['loss'])
# auc
plt.plot(clf.history['train_auc'], label='train')
plt.plot(clf.history['valid_auc'], label='valid')
plt.legend()
plt.show()

# prediction
preds = clf.predict_proba(X_test)
test_auc = roc_auc_score(y_score=preds[:,1], y_true=y_test)

preds_valid = clf.predict_proba(X_valid)
valid_auc = roc_auc_score(y_score=preds_valid[:,1], y_true=y_valid)
print(f"BEST VALID SCORE FOR {dataset_name} : {clf.best_cost}")
print(f"FINAL TEST SCORE FOR {dataset_name} : {test_auc}")

6.jpg
7.jpg
8.jpg
9.jpg

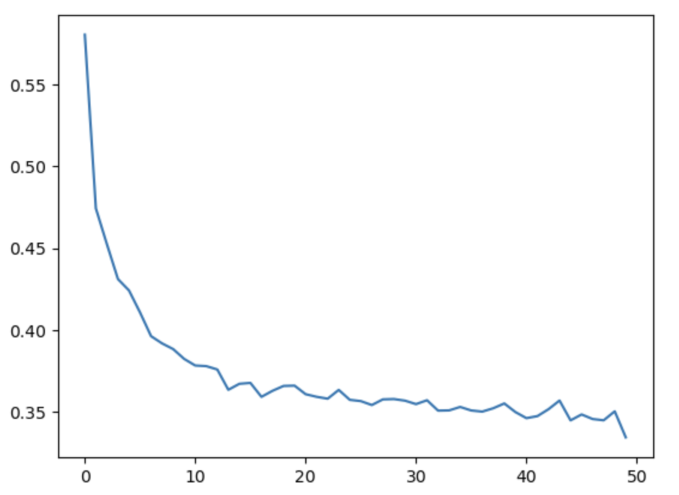
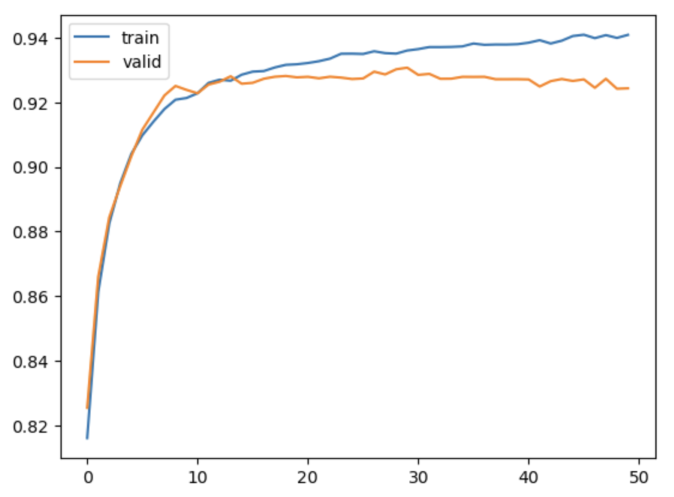
总结

多关注前沿机器学习的内容，会对工作有很大的启发！

引用

TabNet: Attentive Interpretable Tabular Learning
Github 源码

个人备注

此博客内容均为作者学习所做笔记，侵删！
若转作其他用途，请注明来源！