Vgbhfive's Blog

DL-循环神经网络RNN

Posted on Edited on

简介

前面学习了卷积神经网络（CNN），卷积神经网络适合图片这类具有空间局部相关性的数据，而在新的一节中开始学习循环神经网络（RNN），循环神经网络适合具有时间序列的数据，如股票、语音对话、阅读的文本等。

本节内容包含如下：

  • 基本原理
  • 循环神经网络 RNN
  • 长短时记忆网络 LSTM
  • 门控循环网络 GRU

序列表示

序列是指具有先后顺序的一组数据。
序列信号使用一个 shape 为 [b,s] 的张量即可表示，其中 b 表示序列数量，s 表示序列长度。

对于一句含有 n 个单词的句子，单词的表示方法就是之前说过的 one-hot 编码，这种将文字编码为数值的过程叫做 Word Embedding 。
但在此过程中会破坏文字之间的相关性，因此可以通过余弦相关度衡量词向量之间的相关度。
$$ similarity(a, b) = cos(\theta) = {\frac {a * b} {|a| * |b|}} $$

Embedding 层

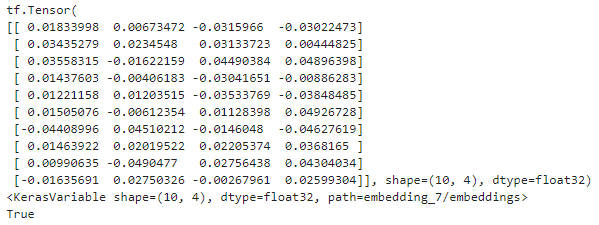
在神经网络总，单词的表示向量可以直接通过训练的方式得到，将单词的表示层称为 Embedding 层。
Embedding 层负责将单词编码为某个词向量 v，其接受的是采用数字编码的单词编号 i，系统总单词量记为 N，输出长度为 n 的向量 v。
Embedding 层实现非常简单，构建一个 shape 为 [N,n] 的查询表对象 table，对于任意的单词编号 i，只需要查询到对应位置上的向量并返回即可。

Embedding 层是可训练的，其放置在神经网络之前，完成单词到向量的转换，得到的表示向量继续通过神经网络完成后续任务，并计算误差 L，采用梯度下降算法来实现端到端（end-to-end）的训练。
通过 layers.Embedding(N, n) 来定义一个 Word Embedding 层，其中 N 表示制定词汇数量，n 指定单词向量长度。 

1
2
3
4
5
6
7
x = tf.range(10) # 生成10个单词的数字编码
x = tf.random.shuffle(x) # 打散
net = layers.Embedding(10, 4) # # 创建共 10 个单词，每个单词用长度为 4 的向量表示的层
out = net(x) 
print(out) # 获取词向量
print(net.embeddings) # 查看 Embedding 层内部的查询表 table
print(net.embeddings.trainable) # 查询表的可优化属性为 True，即可通过梯度下降算法优化

s_1

预训练词向量

Embedding 层的查询表是随机初始化的，需要从零开始训练，但实际上可以使用预训练的 Word Embedding 模型得到更好的单词表示方法。
目前较为广泛的预训练模型为 Word2Vec 和 GloVe 等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# load embedding as a dict
def load_embedding(filename):
    # load embedding into memory, skip first line
    file = open(filename,'r',encoding="utf-8")
    lines = file.readlines()
    file.close()
    # create a map of words to vectors
    embedding = dict()
    for line in lines:
        parts = line.split()
        # key is string word, value is numpy array for vector
        embedding[parts[0]] = asarray(parts[1:], dtype='float32')
    return embedding

# 使用已经训练好的模型参数去初始化 Embedding 层的查询表
embed_glove = load_embedding('glove.6B.50d.txt')
net.set_weights([embed_glove])

经过预训练的词向量模型初始化的 Embedding 层可以设置为不参与训练：net.trainable = False，其预训练的词向量就可以直接应用到此特定任务上。

循环神经网络

原理

如何让网络具有整体理解序列信号的能力？
此时想到了内存（Memory）机制，网络提供一个单独的内存变量，每次提取词向量的特征并刷新内存变量，直至最后一个输入完成，此时的内存变量即存储了所有序列的语义特征，并且由于输入序列之间的先后顺序，使得内存变量内容与序列顺序具有关联。

定义状态向量 $h_0$ 为初始的内存状态，经过 s 个词向量的输入后得到网络最终的状态张量 $h_s$，其很好地代表了句子的全局语义信息，基于 $h_s$ 通过某个全连接层分类器即可完成任务。

循环神经网络

为了解决上述问题，提出了一种新的网络结构。在每个时间戳 $t$，网络层接受当前时间戳的输入 $x$ 和上一个时间戳的网络状态向量 $h$，经过 $h_t = f_{\theta}(h_{t-1}, x_t)$ 变换后得到当前时间戳的新状态向量 $h_t$，并写入内存状态中。

其中 $f_{\theta}$ 表示网络的运算逻辑，在每个时间戳伤网络层均有输出产生 $o = g(h)$，即将网络的状态向量变换后输出。

rnn_1

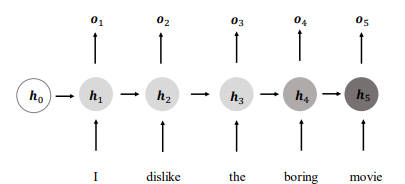
将上述网络结构进行折叠，便可得到网络循环接受序列的每个特征向量 $x_t$，并刷新内部状态向量 $h_t$，同时得到输出 $o_t$，对于这种网络结构将其称为循环网络结构（Recurrent Neural Network, RNN）。

rnn_2

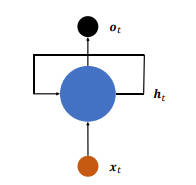
使用 $W_{xh}, W_{hh}, b$ 来参数化 $f$ 网络，并按照
$$ f_{\theta} = \sigma (W_{xh} x_t + W_{hh} h_{t-1} + b) $$
方式更新内存，将这种网络称为基本的循环神经网络。
在循环神经网络中，激活函数一般更多地采用 tanh 函数，并且可以选择不使用偏置 $b$ 来进一步减少参数量。状态向量 $h_t$ 可以直接用作输出，即 $o_t=h_t$，也可以对 $h_t$ 做简单线性变换 $o_t = W_{ho} h_t$ 后得到每个时间戳上的网络输出 $o_t$。

梯度传播

通过循环神经网络的更新表达式可以看出输出对张量 $W_{xh}$、$W_{hh}$ 和偏置 $b$ 均是可导的，其均可以利用自动梯度求导算法计算。

考虑梯度 ${\frac {\delta L} {\delta W_{hh}}}$，由于 $W_{hh}$ 被每个时间戳 i 上权值共享，因此在计算 ${\frac {\delta L} {\delta W_{hh}}}$ 时需要讲每个中间时间戳 i 上的梯度求和，利用链式法则展开为：
$$ {\frac {\delta L} {\delta W_{hh}}} = sum_{i=1}^t {\frac {\delta L} {\delta o_t}} {\frac {\delta o_t} {\delta h_t}} {\frac {\delta h_t} {\delta h_i}} {\frac {\delta^+ h_i} {\delta W_{hh}}} $$

其中 ${\frac {\delta L} {\delta o_t}}$ 可以基于损失函数求得，${\frac {\delta o_t} {\delta h_t}}$ 在 $o_t = h_t$ 时
$${\frac {\delta o_t} {\delta h_t}} = I$$

${\frac {\delta^+ h_i} {\delta W_{hh}}}$ 的梯度将 $h_i$ 展开后也可以求得：
$$ {\frac {\delta^+ h_i} {\delta W_{hh}}} = {\frac {\delta \sigma (W_{xh} x_t + W_{hh} h_{t-1} + b)} {\delta W_{hh}}} $$

其中 ${\frac {\delta^+ h_i} {\delta W_{hh}}}$ 只考虑到一个时间戳的梯度传播，与 ${\frac {\delta L} {\delta W_{hh}}}$ 考虑所有时间戳的偏导数不同，因此只需要推导出 ${\frac {\delta h_t} {\delta h_i}}$ 的表达式即可完成循环神经网络的梯度推导。

利用链式法则将 ${\frac {\delta h_t} {\delta h_i}}$ 拆分为连续时间戳的梯度表达式：
$$ {\frac {\delta h_t} {\delta h_i}} = {\frac {\delta h_t} {\delta h_{t-1}}} {\frac {\delta h_{t-1}} {\delta h_{t-2}}} … {\frac {\delta h_{i+1}} {\delta h_i}} = sum_{k=i}^{t-1} {\frac {\delta h_{k+1}} {\delta h_k}}$$

由于
$$ h_{k+1} = \sigma (W_{xh} x_{k+1} + W_{hh} h_k + b) $$

因此
$$ {\frac {\delta h_{k+1}} {\delta h_k}} = W_{hh}^T diag(\sigma^‘ (W_{xh} x_{k+1} + W_{hh} h_k + b)) = W_{hh}^T diag(\sigma^‘(h_{k+1})) $$

其中 $diag(x)$ 把向量 $x$ 的每个元素作为矩阵的对角元素，得到其他元素全为 0 的对角矩阵。

最终
$$ {\frac {\delta h_t} {\delta h_i}} = sum_{j=i}^{t-1} diag(\sigma^‘(W_{xh} x_{j+1} + W_{hh} h_j + b)) W_{hh} $$

至此 ${\frac {\delta L} {\delta W_{hh}}}$ 梯度推导完成。

梯度爆炸和梯度弥散

循环神经网络的训练并不稳定，其深度并不能随意加深，通过回顾 ${\frac {\delta h_t} {\delta h_i}} = sum_{j=i}^{t-1} diag(\sigma^‘(W_{xh} x_{j+1} + W_{hh} h_j + b)) W_{hh}$ 可以发现其内部包含 $W_{hh}$ 的连乘运算。

  • 当 $W_{hh}$ 的最大值连续大于 1 时，多次相乘会使得 ${\frac {\delta h_t} {\delta h_i}}$ 结果爆炸式增大。
  • 当 $W_{hh}$ 的最大值连续小于 1 时，多次相乘会使得 ${\frac {\delta h_t} {\delta h_i}}$ 结果趋近于零。

这种梯度值接近于 0 的现象叫做梯度弥散（Gradient Vanishing），而把梯度值远大于 1 的现象叫做梯度爆炸（Gradient Exploding）。梯度爆炸和梯度弥散都是神经网络优化过程中很容易出现的情况。

梯度爆炸

梯度爆炸可以通过梯度剪裁（Gradient Clipping）的方式在一定程度上解决。梯度剪裁通过将梯度张量的数值或范数限制在某个较小的区间内，从而将远大于 1 的梯度值减少，避免出现梯度爆炸。

在深度学习中，梯度剪裁常用以下三种方式：

  • 张量的数值限幅
  • 限制梯度张量的范数
  • 全局范数剪裁
梯度弥散

对于梯度弥散现象，可以通过以下措施进行抑制：

  • 增大学习率
  • 减少网络深度
  • 添加 Skip Connection

RNN 层

layers.SimpleRNNCell() 和 layers.SimpleRNN()，其中带 Cell 的层仅完成一个时间戳的前向计算，不带 Cell 的层是基于 Cell 层实现，内部完成多个时间戳的循环计算。

SimpleRNNCell
1
2
3
4
# 特征长度为4，Cell 状态向量特征长度 h=3
cell = layers.SimpleRNNCell(3) # 创建 RNN Cell，内部向量长度为 3
cell.build(input_shape=(None, 4)) # 输出特征长度为 4
cell.trainable_variables # 输出 Wxh, Whh, b 张量

rnn_3

RNN 内部维护 3 个变量，kernel 变量即 $W_{xh}$，recurrent_kernel 变量即 $W_{hh}$，bias 即偏置变量 $b$。

多层 SimpleRNNCell
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x = tf.random.normal([4,80,100])
xt = x[:, 0, :] # 取第一个时间戳的输入 x0
# 构建两个cell，先cell0，再cell1，内存状态向量的长度都是64
cell0 = layers.SimpleRNNCell(64)
cell1 = layers.SimpleRNNCell(64)
h0 = [tf.zeros([4,64])] # cell0 的初始状态向量
h1 = [tf.zeros([4,64])] # cell1 的初始状态向量

# 在时间轴上循环计算多次来实现整个网络的前向计算，每个时间戳上的输入 xt 首先通过第一层， 得到输出o1，然后通过第二层，得到输出o2。
for xt in tf.unstack(x, axis=1):
    o0, h0 = cell0(xt, h0)
    o1, h1 = cell1(o0, h1)
# 上述方式先完成一个时间戳上的输入在所有层上的传播，再循环计算所有时间戳上的输入。

# 需要注意的是，循环神经网络的每一层、每一个时间戳上面均有状态输出，一般取最末层 Cell 的状态作为后续任务网络的输入，因为其最有可能保存高层的全局语义特征。

目前常见的循环神经网络的深度都在10 层以内，因为其很容易出现梯度弥散和梯度爆炸现象。

SimpleRNN
1
2
3
4
layer = layers.SimpleRNN(64) # 创建状态向量长度为64 的SimpleRNN 层
x = tf.random.normal([4,80,100])
out = layer(x) # 一行代码即可获得输出，默认返回最后一个时间戳上的输出
out.shape # [4, 64]

如果希望获得所有时间戳上的输出列表，设置 return_sequences=True 参数

对于多层循环神经网络，可以通过堆叠多个 SimpleRNN 来实现。

1
2
3
4
5
6
7
# 构建两层RNN。出最外层外，均需要返回所有时间戳的输出，用于下一层的输入
net = keras.Sequential([
    layers.SimpleRNN(64, return_sequences=True),
    layers.SimpleRNN(64)
])
out = net(x) # 前向计算
out.shape # [4, 64]

RNN 短时记忆

循环神经网络在处理较长的句子时，仅能够理解有限长度内的信息，而对于较长范围内的信息往往不能很好利用，这种现象被叫做短时记忆。
那该如何延长短时记忆？就提出了长短时记忆网络（Long Short-Term Memory, LSTM) ，相比 RNN 其记忆能力更强，更擅长处理较长的序列信号数据。

LSTM

相比 RNN 网络只有一个状态向量 $h_t$，LSTM 新增了一个状态向量 $C_t$，同时引入门控（Gate）机制，可通过门控单元来控制信息的遗忘和刷新。
在 LSTM 中有两个状态向量 c 和 h，其中 c 作为 LSTM 的内部状态向量，可以理解为 LSTM 的内存状态向量 Memory；而 h 表示 LSTM 的输出向量。同时 LSTM 将内部 Memory 和输出分开为两个变量，利用以下三个门控来控制内部信息的流动：

  • 输入门（Input Gate）
  • 遗忘门（Forget Gate）
  • 输出门（Output Gate）

门控机制

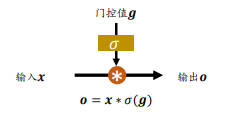
门控机制可以简单理解为控制数据流通量的一种手段。
在 LSTM 中阀门的开合程度通过门控值向量 g 表示，通过 $\sigma_g$ 激活函数将门控制压缩到 [0,1] 之间区间。

  • 当 $\sigma_g=0$ 时，门控值全部关闭，输出 o=0。
  • 当 $\sigma_g=1$ 时，门控全部打开，输出 o=x。

通过门控机制可以较好地控制数据的流量程度。

lstm_1

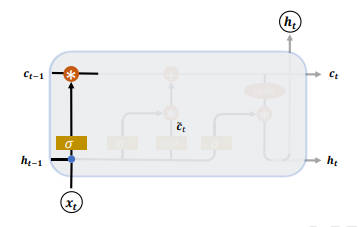
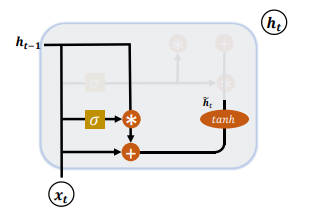
输入门

输入门用于控制 LSTM 对输入的接收程度。
首先通过对当前时间戳的输入 $x_t$ 和上一个时间戳的输出 $h_{t-1}$ 做非线性变换得到新的输入变量 $\hat{c_t}$
$$\hat{c_t} = tanh(W_c[h_{t-1}, x_t] + b_c)$$

其中 $W_c$ 和 $b_c$ 为输入门的参数，需要通过反向传播算法自动优化，tanh 为激活函数，用于将输入标准化到 [-1,1] 区间。
$\hat{c_t}$ 并不会全部刷新进入 LSTM 的 Memory，而是通过输入门控制接受输入的量。

输入门的控制变量同样来自于输入 $x_t$ 和输出 $h_{t-1}$：
$$g_i = \sigma(W_i[h_{t-1},x_t] + b_i)$$

其中 $W_i$ 和 $b_i$ 为输入门的参数，需要通过反向传播算法自动优化，$\sigma$ 为激活函数，一般使用 Sigmoid 函数。
输入门控制变量 $g_i$ 决定了 LSTM 对当前时间戳的新输入 $\hat{c_t}$ 的接受程度：

  • 当 $g_i=0$ 时，LSTM 不接受任何的新输入 $\hat{c_t}$。
  • 当 $g_i=1$ 时，LSTM 全部接受新输入 $\hat{c_t}$。

经过输入门后，待写入 Memory 的向量为 $g_i * \hat{c_t}$。

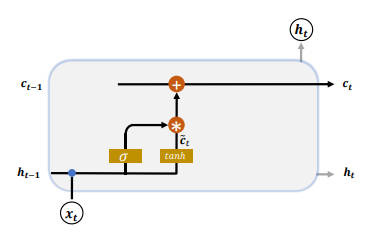
lstm_2

遗忘门

遗忘门作用于 LSTM 状态向量 c 上，用于控制上一个时间戳的记忆 $c_{t-1}$ 对当前时间戳的影响。
遗忘门的控制变量 $g_f$
$$g_f = \sigma(W_f[h_{t-1}, x_t] + b_f)$$

其中 $W_f$ 和 $b_f$ 为遗忘门的参数张量，可由反向传播算法自动优化，$\sigma$ 为激活函数，一般使用 Sigmoid 函数。

  • 当门控 $g_f=1$ 时，遗忘门全部打开，LSTM 接受上一个状态 $c_{t-1}$ 的所有信息；
  • 当门控 $g_f=0$ 时，遗忘门关闭，LSTM 直接忽略 $c_{t-1}$，输出为 0 的向量。

经过遗忘门后，LSTM 的状态向量变为 $g_f * c_{t-1}$。

lstm_3

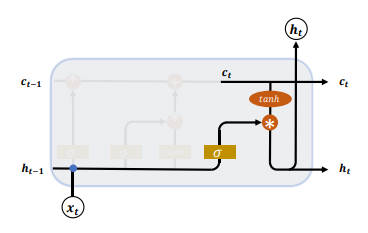
输出门

LSTM 的内部状态向量 $c_t$ 并不会直接用于输出，这一点与 RNN 不一样。RNN 网络的状态向量 h 即用于记忆，也用于输出，因此 RNN 可以理解为状态向量 c 和输出向量 h 是同一个对象。

LSTM 中状态向量并不会全部输出，而是在输出门作用下选择性地输出。输出门的门控变量 $g_o$ 为
$$g_o = \sigma(W_o[h_{t-1},x_t] + b_o)$$

其中 $W_o$ 和 $b_o$ 为输出门的参数，通过需要通过反向传播算法自动优化，$\sigma$ 为激活函数，一般使用 Sigmoid 函数。

  • 当输出门 $g_o=0$ 时，输出关闭，LSTM 的内部记忆完全被隔断，无法用作输出，此时输出向量为 0。
  • 当输出门 $g_o=1$ 时，输出完全打开，LSTM 的状态向量 $c_t$ 全部用于输出。

LSTM 的输出
$$h_t = g_o*tanh(c_t)$$

即内存向量 $c_t$ 经过 tanh 激活函数后与输入门作用得到 LSTM 的输出。$g_o \in [0,1]$ 同时 $tanh \in [-1,1]$，因此 LSTM 的输出 $h_t \in [-1,1]$。

lstm_4

刷新 Memory

在遗忘门和输入门的控制下，LSTM 有选择地读取上一个时间戳的记忆 $c_{t-1}$ 和当前时间戳的新输入 $\hat{c_t}$，状态向量 $c_t$ 的刷新方式为：
$$c_t = g_i * \hat{c_t} + g_f * c_{t-1}$$

得到新的状态向量 $c_t$ 即为当前时间戳的状态向量。

小结

LSTM 虽然状态向量和门控数量较多，计算流程复杂，但将典型的门控列表列举出来，即可解释 LSTM 的行为。

输入门控 遗忘门控 LSTM 行为
0 1 只使用记忆
1 1 综合输入和记忆
0 0 清零记忆
1 0 输入覆盖记忆

LSTM 层

在 TensorFLow 中同样有两种方式实现 LSTM 网络。既可以使用 LSTMCell 来手动完成时间戳上面的循环运算，也可以通过 LSTM 层方式一步完成前向计算。

LSTMCell

新建一个状态向量长度为 64 的 LSTMCell，其中状态向量 $c_t$ 和输出向量 $h_t$ 的长度均为 h。

1
2
3
4
5
6
7
8
9
10
x = tf.random.normal([2,80,100])
xt = x[:, 0, :] # 得到第一个时间戳的输入
cell = layers.LSTMCell(64) # 创建 LSTMCell
state = [tf.zeros([2,64]), tf.zeros([2,64])] # 初始化状态和输出list
out, state = cell(xt, state) # 前向计算
id(out), id(state[0]), id(state[1]) # out 和 list 的第一个元素的 id 相同

# 通过在时间戳上展开循环运算，即可完成一次层的前向传播
for xt in tf.unstack(x, axis=1):
    out, state = cell(xt, state) # 前向计算

lstmcell_1

LSTM

通过 layers.LSTM 层可以方便地一次完成整个序列的运算。

1
2
3
layer = layers.LSTM(64) # 创建一层 LSTM 层，内存向量长度为 64
out = layer(x) # 序列通过 LSTM 层，默认返回最后一个时间戳的输出 h
out.shape # [[2, 64]]

默认返回最后一个时间戳的输出，如果需要返回所有时间戳的输出，需要设置 return_sequences=True 标志

对于多层神经网络，可以通过 Sequential 容器包裹多层 LSTM 层，并设置所有非模型网络 return_sequences=True，这是因为非末层需要上一层在所有时间戳的输出作为输入。

1
2
3
4
5
6
net = Sequential([
    layers.LSTM(64, return_sequences=True), # 非末层需要返回所有时间戳输出
    layers.LSTM(64)
])
out = net(x)
out.shape # [2, 64]

GRU

LSTM 由于其门控机制可以在大部分序列任务取得较好的性能表现，但结构相对复杂、计算代价高、模型参数量较大等问题则有了门控循环网络（Gated Recurrent Unit, GRU），其可以理解为是 LSTM 的简化版本。
GRU 通过将内部状态向量和输出向量合并，统一为状态向量 h，同时门控数量也减少到两个：

  • 复位门（Reset Gate）
  • 更新门（Update Gate）

复位门

复位门用于控制上一个时间戳的状态 $h_{t-1}$ 进入 GRU 的量。
门控向量 $g_r$ 由当前时间戳的输入 $x_t$ 和上一个时间戳状态 $h_{t-1}$ 变换而得
$$g_r=\sigma(W_r[h_{t-1}, x_t] + b_r)$$

其中 $W_r$ 和 $b_r$ 为复位门的参数，由反向传播算法自动优化，$\sigma$ 为激活函数，一般使用 Sigmoid 函数。

门控向量 $g_r$ 仅控制状态 $h_{t-1}$，而不会控制输入 $x_t$
$$\hat{h_t} = tanh(W_h[g_r h_{t-1}, x_t] + b_h)$$

  • 当 $g_r=0$ 时，新输入 $\hat{h_t}$ 全部来源于输入 $x_t$，不接受 $h_{t-1}$，此时相当于复位。
  • 当 $g_r=1$ 时，$h_{t-1}$ 和 $x_t$ 共同作用产生新输入 $\hat{h_t}$。

gru_1

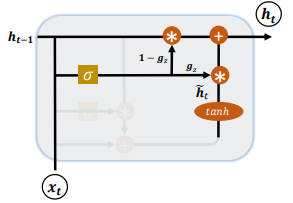
更新门

更新门控制上一个时间戳转台 $h_{t-1}$ 和新输入 $\hat{h_t}$ 对新状态向量 $h_t$ 的影响程度。更新门控向量 $g_z$
$$g_z = \sigma(W_z[h_{t-1}, x_t] + b_z)$$

其中 $W_z$ 和 $b_z$ 为更新门的参数，由反向传播算法自动优化，$\sigma$ 为激活函数，一般使用 Sigmoid 函数。

$g_z$ 用于控制新输入 $\hat{h_t}$，$1-g_z$ 用于控制状态 $h_{t-1}$：
$$ h_t = (1-g_z) * h_{t-1} + g_z * \hat{h_t} $$

由上面可以看出 $h_{t-1}$ 与 $\hat{h_t}$ 处于此消彼长的状态，相互竞争。

  • 当更新门 $g_z=0$ 时，$h_t$ 全部来自上一个时间戳状态 $h_{t-1}$。
  • 当更新门 $g_z=1$ 时，$h_t$ 全部来自新输入 $\hat{h_t}$。

gru_2

GRU 层

GRUCell

同样地也有 Cell 方式和层方式实现 GRU 网络。

1
2
3
4
5
h = [tf.zeros([2,64])] # 初始化状态向量，GRU 只有一个
cell = layers.GRUCell(64) # 新建 GRUCell，向量长度64
for xt in tf.unstack(x, axis=1):
    out, h = cell(xt, h)
out.shape # [2,64]
GRU

使用 Sequential 容器堆叠多层 GRU 层的网络。

1
2
3
4
5
6
net = Sequential([
    layers.GRU(64, return_sequences=True),
    layers.GRU(64)
])
out = net(x)
out.shape # [2,64]

实践

本次实践使用最基础的 RNN 来实现情感分类。
RNN 网络共两层，循环提取序列信号的语义特征，利用第二层 RNN 层的最后时间戳的状态向量 $h_s$ 作为句子的全局语义特征表示，之后送入全连接层构成的分类网络，得到样本为 $x$ 为积极情感的概率 $P$。

SimpleRNN 模型

引入依赖
1
2
3
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, optimizers, losses, Sequential
加载数据
1
2
3
4
5
6
7
8
9
# 数据集
batchsz = 128 # 批量大小
total_words = 10000 # 词汇表大小
max_review_len = 80 # 句子最大长度s
embedding_len = 100 # 词向量特征长度n

(x_train, y_train), (x_test, y_test) = keras.datasets.imdb.load_data(num_words=total_words)
print(x_train.shape, len(x_train[0]), y_train.shape)
print(x_test.shape, len(x_test[0]), y_test.shape)

p_1

预处理数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 数字编码表
word_index = keras.datasets.imdb.get_word_index()
for k, v in word_index.items():
    print(k,v) # 输出编码表的单词和对应的数字

# 添加标志位ID
word_index = {k:(v+3) for k,v in word_index.items()}
word_index['<PAD>'] = 0 # 填充标志
word_index['<START>'] = 1 # 起始标志
word_index['<UNK>'] = 2 # 未知单词的标志
word_index['<UNUSED>'] = 3

# 翻转码表
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])

# 定义函数，将数字转换为字符串
def decode_review(text):
    return ' '.join([reverse_word_index.get(i, '?') for i in text])
decode_review(x_train[0])

# 对于长度参差不齐的句子进行截断、填充处理
x_train = keras.preprocessing.sequence.pad_sequences(x_train, maxlen=max_review_len)
x_test = keras.preprocessing.sequence.pad_sequences(x_test, maxlen=max_review_len)

# 截断或填充等长句子后，通过 Dataset 类包裹成数据集对象
db_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))
db_train = db_train.shuffle(1000).batch(batchsz, drop_remainder=True) # drop_remainder 参数设置丢弃最后一个 Batch
db_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
db_test = db_test.shuffle(1000).batch(batchsz, drop_remainder=True)
print(x_train.shape, tf.reduce_max(y_train), tf.reduce_min(y_train))

p_2

模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 网络模型
class MyRNN(keras.Model):
    # Cell 方式构建多层网络
    def __init__(self, units):
        super(MyRNN, self).__init__()
        # [b,64] 构建 Cell 初始化状态向量
        self.state0 = [tf.zeros([batchsz, units])]
        self.state1 = [tf.zeros([batchsz, units])]
        # 词向量编码 [b,80] -> [b,80,100]
        self.embedding = layers.Embedding(total_words, embedding_len, input_length=max_review_len)
        # 构建两个 Cell，使用 Dropout 防止过拟合
        self.cell0 = layers.SimpleRNNCell(units, dropout=0.5)
        self.cell1 = layers.SimpleRNNCell(units, dropout=0.5)
        # 构建分类网络，用于将 Cell 的输出特征进行分类 [b, 80, 100] -> [b, 64] -> [b, 1]
        self.outlayer = Sequential([
            layers.Dense(units),
            layers.Dropout(rate=0.5),
            layers.ReLU(),
            layers.Dense(1)
        ])
    
    def call(self, inputs, training=None):
        # [b,80]
        x = inputs
        # 获取词向量 [b,80] -> [b,80,100]
        x = self.embedding(x)
        # 通过两个 Cell [b,80,100] -> [b,64]
        state0 = self.state0
        state1 = self.state1
        # word: [b,100]
        for word in tf.unstack(x, axis=1):
            out0, state0 = self.cell0(word, state0, training)
            out1, state1 = self.cell1(out0, state1, training)
        # 末层最后一个输出作为分类网络的输入 [b,64] -> [b,1]
        x = self.outlayer(out1, training)
        # 激活函数
        prob = tf.sigmoid(x)
        return prob
训练模型并计算准确率
1
2
3
4
5
6
7
8
9
10
11
12
# 训练与测试
units = 64 # RNN 状态向量长度
epochs = 20 # 训练epochs

# 创建模型
model = MyRNN(units)
# 装配
model.compile(optimizer=optimizers.Adam(0.001), loss=losses.BinaryCrossentropy(), metrics=['accuracy'])
# 训练与验证
model.fit(db_train, epochs=epochs, validation_data=db_test)
# 测试
model.evaluate(db_test)

p_3

在经历 20 轮次训练后，其在测试集上的准确率可以轻松达到 79.02%。

LSTM/GRU 模型

得益于 TensorFlow 在循环神经网络相关接口的统一，原有代码仅需修改少部分即可升级到 LSTM 模型或 GRU 模型。

LSTM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 网络模型
class MyRNN(keras.Model):
    # Cell 方式构建多层网络
    def __init__(self, units):
        super(MyRNN, self).__init__()
        # [b,64] 构建 Cell 初始化状态向量
        self.state0 = [tf.zeros([batchsz, units]), tf.zeros([batchsz, units])]
        self.state1 = [tf.zeros([batchsz, units]), tf.zeros([batchsz, units])]
        # 词向量编码 [b,80] -> [b,80,100]
        self.embedding = layers.Embedding(total_words, embedding_len, input_length=max_review_len)
        # 构建两个 Cell，使用 Dropout 防止过拟合
        self.cell0 = layers.LSTMCell(units, dropout=0.5)
        self.cell1 = layers.LSTMCell(units, dropout=0.5)
        # 构建分类网络，用于将 Cell 的输出特征进行分类 [b, 80, 100] -> [b, 64] -> [b, 1]
        self.outlayer = Sequential([
            layers.Dense(units),
            layers.Dropout(rate=0.5),
            layers.ReLU(),
            layers.Dense(1)
        ])
    
    def call(self, inputs, training=None):
        # [b,80]
        x = inputs
        # 获取词向量 [b,80] -> [b,80,100]
        x = self.embedding(x)
        # 通过两个 Cell [b,80,100] -> [b,64]
        state0 = self.state0
        state1 = self.state1
        # word: [b,100]
        for word in tf.unstack(x, axis=1):
            out0, state0 = self.cell0(word, state0, training)
            out1, state1 = self.cell1(out0, state1, training)
        # 末层最后一个输出作为分类网络的输入 [b,64] -> [b,1]
        x = self.outlayer(out1, training)
        # 激活函数
        prob = tf.sigmoid(x)
        return prob

p_4

GRU
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 网络模型
class MyRNN(keras.Model):
    # Cell 方式构建多层网络
    def __init__(self, units):
        super(MyRNN, self).__init__()
        # [b,64] 构建 Cell 初始化状态向量
        self.state0 = [tf.zeros([batchsz, units])]
        self.state1 = [tf.zeros([batchsz, units])]
        # 词向量编码 [b,80] -> [b,80,100]
        self.embedding = layers.Embedding(total_words, embedding_len, input_length=max_review_len)
        # 构建两个 Cell，使用 Dropout 防止过拟合
        self.cell0 = layers.GRUCell(units, dropout=0.5)
        self.cell1 = layers.GRUCell(units, dropout=0.5)
        # 构建分类网络，用于将 Cell 的输出特征进行分类 [b, 80, 100] -> [b, 64] -> [b, 1]
        self.outlayer = Sequential([
            layers.Dense(units),
            layers.Dropout(rate=0.5),
            layers.ReLU(),
            layers.Dense(1)
        ])
    
    def call(self, inputs, training=None):
        # [b,80]
        x = inputs
        # 获取词向量 [b,80] -> [b,80,100]
        x = self.embedding(x)
        # 通过两个 Cell [b,80,100] -> [b,64]
        state0 = self.state0
        state1 = self.state1
        # word: [b,100]
        for word in tf.unstack(x, axis=1):
            out0, state0 = self.cell0(word, state0, training)
            out1, state1 = self.cell1(out0, state1, training)
        # 末层最后一个输出作为分类网络的输入 [b,64] -> [b,1]
        x = self.outlayer(out1, training)
        # 激活函数
        prob = tf.sigmoid(x)
        return prob

p_5

对比 RNN、LSTM、GRU 三者在测试集上的准确率，可以发现每次技术上的优化都会带来实实在在的提升。

总结

所有事物都是基于已有旧事务之上优化、演进而来，对于计算机技术也是如此！

最近新发布了 Test Time Training(TTT): RNNs with Expressive Hidden States，有兴趣的可以去研究下。

引用

个人备注

此博客内容均为作者学习《TensorFlow深度学习》所做笔记，侵删！
若转作其他用途，请注明来源！