智能风控-风控模型体系

概述

风控模型是风控系统的核心，应用模型进行风险决策是识别风险的主要途径，也是控制风险的重要方法。

在信贷风控领域中 模型主要是指预测风险的方法，通常以数学公式或行数的方式存在。
这其中模型和算法不可混为一谈，算法通常是指各种数学、统计或人工智能方法，而模型是指基于这些方法得到的具体实例；因此才会出现使用了某种算法构建多个风险模型。假设两者相比较的话，可以将算法比作类，而模型则是 实例对象。

构建风控模型并不是 必须 使用机器学习算法，如策略人员基于人工经验和统计分析，利用 评分卡模型 来汇总各类风险指标，赋予各类风险指标一个分数之后，最后汇总即可。但这种方法也存在弊端，即无法处理更多维度的数据，也很难处理不同维度数据之间的关联信息，评估准确性较低、局限性很大。因此随着技术的发展，机器学习方法逐渐成为主要的建模方法。

机器学习是一种从历史数据中学习潜在规律，同时预测未来行为的方法。其核心的三要素：数据、模型、算法。其中数据和算法是搭建机器学习模型的 必要条件，每种算法都包含多个待定的参数或结构，模型是算法在数据上运算得到特定的参数或结构的 结果。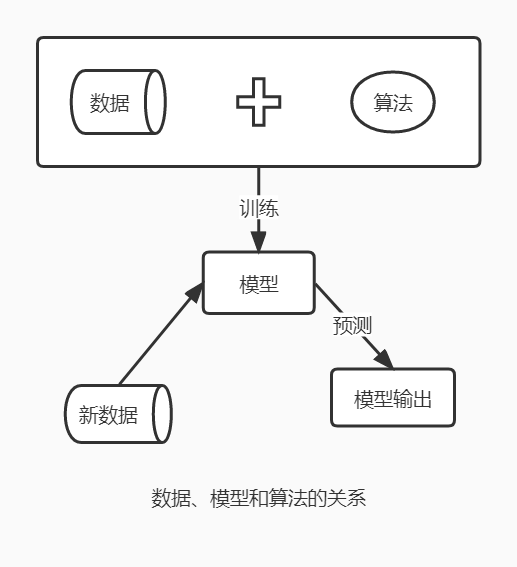

其中根据数据集中是否已知样本标签，机器学习任务又可以分为：有监督学习是指从有标签的训练数据中学习；无监督学习是指从无标签的训练数据中学习。
有标签的训练数据是指每个训练样本都包含输入和期望的输出；相反无标签则是指每个训练样本只包含输入不包含输出。

采用多种机器学习算法搭建风控模型的主要步骤都是相同的，主要包含以下几个步骤：

• 问题定义
• 样本的选择与划分
• 模型架构设计
• 数据准备与描述分析
• 数据清洗
• 特征选择
• 模型训练与效果评估
• 部署上线
• 模型监控与异常处理
• 模型调优

---

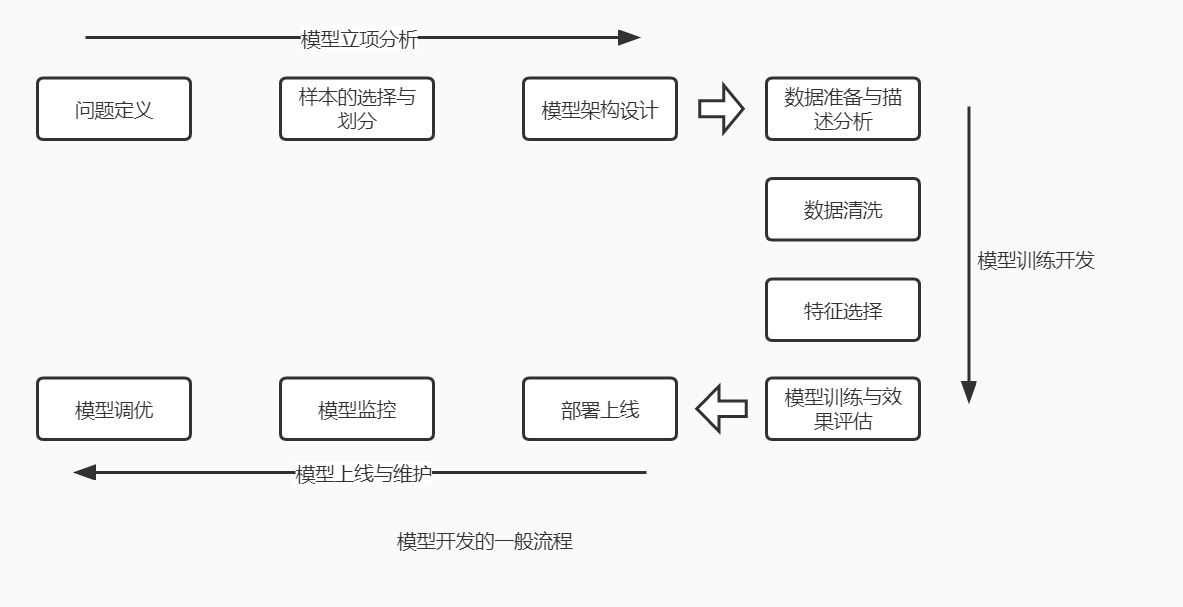
开发方法论

开发好样本是开发好模型的基础。构建好样本是指从项目需求中定义问题、定义标签、选择合适的建模数据集以及分析和预处理数据的过程。
构建好模型是指在经过预处理的数据中进行特征选择、特征提取、模型训练、分数转化和效果评估。

---

开发方法论-立项分析

问题定义

问题定义旨在明确项目的背景和目标，根据背景和目标将业务问题转化为机器学习建模问题，包括定义预测目标、设计模型方案等。
在实际业务中开始分析目标时需要先了解预测对象粒度、标签定义和细分客群。

1. 预测对象粒度
   在实际业务中会遇到不同层次的问题，基于不同层次的问题，需要将预测对象定义为不同的粒度。因此在实际业务中，需要根据业务模式和模型应用策略来选择合适的粒度进行建模。

   • 渠道粒度，某些场景下借款申请人来自于同一个渠道，即一个渠道一条记录。
   • 客户粒度，借款人存在多笔借款，从借款人角度考虑风险即任何一笔借款出现逾期都表示风险事件，即一个人是一条记录。
   • 借款粒度，借款人的每次申请借款考虑风险，该笔借款出现逾期则表现出风险事件，即一次借款就是一条记录。
   • 还款粒度，每个借款人得到每一次借款可能都有不同的还款期限，预测每笔还款是否出现风险，即一次还款就是一条记录。

2. 标签定义
   风控模型用来预测未来的风险是典型的有监督学习模式，因此需要定义样本标签。
   标签是模型所要预测的结果，可以是二分类结果，例如“好”/“坏”、“响应”/“不响应”等；也可以是连续变量，例如收益、损失等。风险评估模型通常用来预测未来的表现是好是坏，其中标签定义需要明确的是在什么时间点预测未来多久发生的什么事件。
   观测点前后分别是观察窗口和表现窗口。

   • 观察窗口，用来观察客户行为的时间区间。观察窗口也称为观察期。
   • 表现窗口，用来考察客户的表现，从而确定标签定义的时间区间。表现窗口也称为表现期。

   在风险标签定义中，对于如何确定好坏程度和表现窗口的长度，需要结合滚动率分析（roll rate analysis）和账龄分析（vintage analysis）。

   • 滚动率分析，通过滚动率分析来确定客户的“好坏”程序。滚动率是指客户从某个观测点之前的一段时间的逾期状态向观测点之后的一段时间的逾期状态转化的比例。
   • 账龄分析，信贷行业经常使用 Vintage 曲线分析账户的成熟期、变化规律等。Vintage 曲线是根据账龄绘制的不同时间放款样本的逾期率变化曲线。逾期率有金额逾期和账单逾期两种口径。

   综上所述，滚动率分析用于分析客户的“好坏”程度；账龄分析用于确定合适的表现期，可以尽可能多地覆盖“坏”客户。

3. 细分客群
   在建模任务中如果客群差异较大则需要进一步细分客群。根据不同产品拆分客群时，不同的进件渠道、借款期数、区域和借款金额等划分客群。除此之外还可以采用聚类等无监督学习方法划分客群。
   至此细分客群建模还需要满足下列条件：

   • 细分客群之间的风险水平差异较大。
   • 细分客群可以获得的特征维度不同。
   • 每个细分客群的样本足够多。

   通过细分客群建模可以使模型更加专注于细分客群风险模式的学习，从而提高模型效果。不过细分客群建模也存在弊端：细分客群建模会导致模型数量增多，需要投入的资源和时间增多，维护成本增加；细分客群将总样本分散到各个客群中，相比总样本量细分客群样本量减少，特别是细分客群的“坏”样本量不多，反而会降低模型的预测能力。

样本的选择与划分

1. 样本选择
   样本选择是指从业务数据选择部分合适的样本进行模型开发。
   风控模型是一种预测模型，保证模型良好的预测效果的前提是客户未来的行为和过去相似，因此才可以从过去的数据中学习规律并预测未来的表现。其中选取的建模样本需要把握建模样本必须能够代表总体，与未来模型使用场景下的样本差异尽可能小，具体体现为以下四点：代表性；充分性；时效性；排除性。

2. 样本集划分
   数据是模型搭建的基础。
   在模型开发过程中会将一部分数据划分用于训练模型，另一部分数据划分为验证模型效果。总体数据可以划分为训练集、验证集和测试集，其中训练集用于训练模型，验证集用来模型调参、训练过程中的参数选择或者模型选择，测试集用来验证模型最终表现（通常选用靠近当前时间的样本作为测试集，也称 OOT（Out of Time sample） 样本）。典型的训练样本、验证样本、OOT 样本划分比例是 7:2:1。
   在特殊并且样本较少时，为了让更好的样本参与模型训练，可以将验证样本取消，保留训练样本和 OOT 样本，训练时采用交叉验证的方式进行模型参数选择。另外避免出现异常，可以先 空跑 一段时间观察模型情况。

架构设计

在明确问题定义、确定样本和样本集划分之后，模型搭建的基本任务已经清晰，关于如何更好的预测目标，需要首先从宏观上考虑模型的架构。
从模型数据源维度考虑，模型架构可以分为：

• 单一模型架构
  不区分数据源，将所有数据源特征放在一起进行建模，输出最终模型。
• 多子模型融合架构
  将不同维度的数据源划分为若干个集合，先建立子模型，再将子模型进行二次融合，生成最终模型。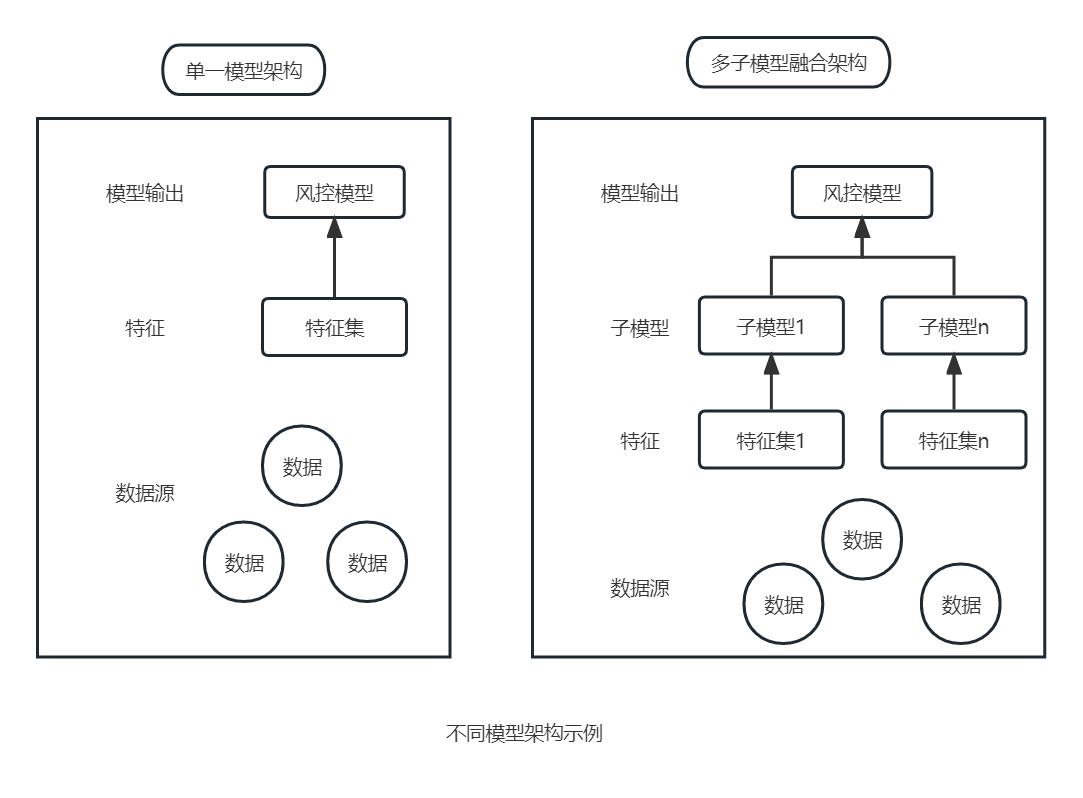
  

模型架构除了可以从数据源维度进行划分之外，还可以：

• 从目标逾期标签定义或表现期长短的角度，分别建立 DPD10 逾期模型、DPD60 逾期模型，长表现期子模型和短表现期子模型等。
• 结合客群细分，建立基于不同细分客群的子模型，再进行二次融合。
• 采用不同算法建立不同子模型，再进行二次融合。

在实际业务条件下，面对的可变条件太多、数据量的大小、模型调参方法的差异和特征维度的差异都会导致模型结果出现偏差，因此在同等条件下可以采用如无必要，勿增实体的原则，即采用最简单的方案。

---

开发方法论-训练开发

数据的准备和描述

1. 数据准备
   数据准备是将构造完整的建模数据集，数据集的每一列为一个特征。风控模型中的特征是根据预测目标的粒度，基于底层的原始数据，通过汇总等方式加工而成的。而由于底层数据的不同，特征一般会分为不同的模块，每个特征模块包含若干个特征。

   在数据准备阶段将可用的特征模块逐一按照样本选择的范围和每个样本观测点计算出对应的特征。通常将事后计算以前某个时间点的特征的行为称为回溯。特别的需要确保特征数据是观测点时刻可以获取的当时状态，这样才能保证模型在应用时才能获取到相同的特征。当原始数据已经被修改，无法追溯到当时的特征时，特征就不能 回溯，因此也就无法使用此特征。

   特征无法回溯而造成特征值中包含观测点之后的信息，这被称为特征穿越或信息泄露。这种问题通常导致的后果就是特征效果和模型效果异常好，当真实场景使用时并不能得到相同的效果。因此特征穿越问题需要尽可能在数据准备阶段尽力排除，排除此问题共有以下三种方法：

   • 回溯数据与线上实时计算数据的一致性检查。
   • 单个变量与预测标签的效果指标分析。
   • 单个样本特征计算逻辑分析。

2. 数据描述
   数据描述即探索性数据分析（Exploratory Data Analysis, EDA）是指对特征进行统计分析，统计每个特征的缺失率、唯一值个数、最大值、最小值、平均值和趋势性变化等指标，使模型开发人员对数据集有清晰、细致的了解。
   数据描述的目的在于了解特征分布，确认数据质量，在得到所有特征的统计指标后，需要首先确认数据质量，分析每个指标是否合理，而非直接进行数据清洗。

   数据问题通常包含两类：

   • 由于非正常因素导致的异常，如系统故障导致的数据缺失。
   • 业务调整导致的异常，业务调整对某些特征是否影响的，会造成特征分布偏移。

数据预处理（清洗）

在进行特征选择和构建模型之前需要对数据进行预处理，使得数据能够全面反映全体样本信息，以适用于机器学习模型。
数据预处理包含异常值处理、特征缺失值处理、特征无量纲化、连续特征离散化、类别特征数值化和特征交叉组合。

1. 异常值处理
   在实际业务中由于种种因素，通常会遇到异常值，如果不处理这些异常值将会导致后续数据分析和模型训练出现严重误差。

   • 异常值检测
     异常值检测主要有三种方法：

     • 基于统计的方法。基于统计的方法一般会构建一个概率分布模型，并计算对象符合该模型的概率，把具有低概率的对象视为异常点。
     • 基于聚类的方法。基于聚类算法将训练样本划分为若干类，如果某一个类的样本数很少，而且类中心和其他类的距离都很远，那么这个类中的样本极有可能就是异常点。
     • 专业的异常点检测算法。孤立森林（lsolation Forest）是一种应用官方的异常点检测算法。

   • 异常值处理
     在检测出异常值后，一般常见的处理方式有两种：

     • 直接删除包含异常值的样本。
     • 结合特征含义选择置空异常值，或者填充为其他值。

     另外有两种“异常”是无法通过技术手段检测出来的，需要结合具体业务含义识别

     • 周期性变化的特征。这类特征会严重影响模型的稳定性，应予以剔除。
     • 具有明显缺陷的特征，如有些埋点后续不会再有，相关特征应予以剔除。

   需要强调的是处理异常值必须谨慎。通过算法筛选出的异常值是否真正异常，需要从业务含义角度再次确认，避免将正常数据过滤掉。

2. 特征缺失值处理
   在处理特征缺失值之前，需要先判断缺失的原因。在实际业务中，出现缺失的原因有两种：

   • 非正常缺失。是指由于原始数据存储、数据接口出现异常而导致的回溯的特征缺失。
   • 正常缺失。对于需要客户授权的数据，部分客户拒绝会导致数据缺失；另外特殊的特征计算也会造成特征缺失。特征缺失值是否需要填充，需要根据建模时使用的算法综合考虑。
     • 使用线性回归算法时，可以根据特征含义使用均值、众数和中位数等填充。
     • 在使用逻辑斯谛回归建立传统评分卡模型时，由于模型训练前会对特征进行分箱处理，因此会将特征缺失值单独作为一箱。
     • 使用决策树建模时，例如 XGBoost 算法会自动处理特征缺失值，因此不需要填充。

   不同缺失的处理方案如下：

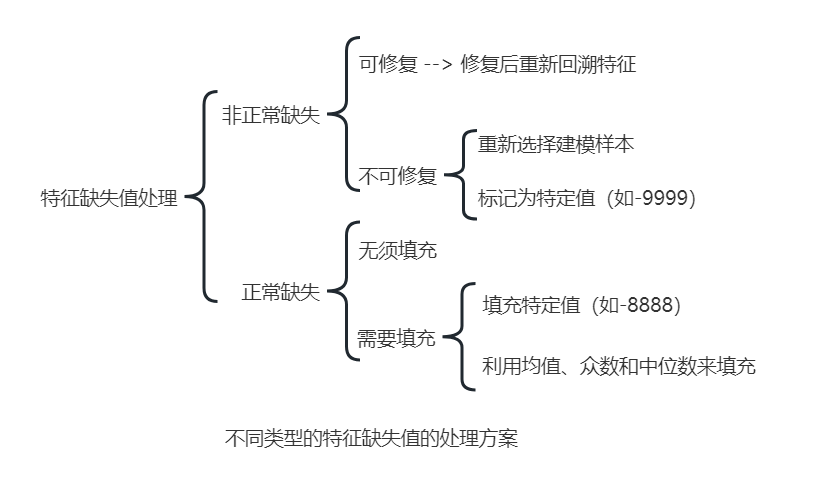
3. 特征无量纲化
   特征无量纲化主要是通过特征的标准化将特征“缩小”到同一量纲。
   对于建模特征，如果特征的单位或大小相差较大，或者特征的方差比其他几个特征高几个数量级，那么就很容易影响目标结果，使得线性模型无法学习其他特征，此时有必要进行特征标准化处理。常见的标准化处理方式如下：

   • max-min 标准化
     max-min 标准化也称为“归一化”，是通过对原始特征进行变换，把特征值映射到 [0, 1]。其中 Xmax 表示特征最大值，Xmin 表示特征最小值，X 表示原始特征值，变换公式如下：

     X' = (X - Xmin) / (Xmax - Xmin)

   • z-score 标准化
     z-score 标准化是常见的特征预处理方式，线性模型在训练数据之前基本都会进行 z-score 标准化。对原始特征进行变换可以把特征分布变换到均值为 0，标准差为 1，变换公式如下所示，其中 u 为特征均值，a 为特征标准差。

     X' = (X - u) / a

   在使用 max-min 标准化时，如果测试集里的特征存在小于 Xmin 或大于 Xmac 的值，就会导致 Xmin 和 Xmax 发生变化。

4. 连续特征离散化
   连续特征离散化也称特征分箱，是指将连续属性的特征进行分段，使其变成一个个离散的区间。
   在使用逻辑斯谛回归建立风控评分卡模型时，通常会对来连续特征进行离散化分箱，离散化后的特征对异常值有很强的鲁棒性，降低模型过拟合的风险，模型会更加稳定。此外单个特征离散化为多个分箱之后，再对分箱进行数值转换（例如 WOE 转换），此过程可以对非线性的关系进行线性转化，提高线性模型的表达能力。当建模的样本量较少时，离散化特征就非常重要，经过离散化后可以丢弃数据的细节信息，有效降低过拟合风险。
   常见的特征分箱如下：

   • 等频分箱是指分箱后，每个箱内的样本量相等。等频分箱能够确保每箱有足够的样本量，更有统计意义且在实际种应用广泛。
   • 等距分箱是指按照相同宽度将特征值分为若干等份，各箱的特征值跨度相同。等距分箱的缺点是受到异常值的影响比较大，各箱之间的样本量不均衡，甚至有可能出现箱的样本量为 0 的情况。
   • 卡方分箱是依赖于卡方校验的分箱方法，其基本思想是判断相邻的两个区间是否有分布差异，基于卡方统计量的结果进行自下而上的合并，直到满足分箱的终止条件为止。终止条件包括分箱个数和卡方阈值。
   • 决策树分箱是指利用决策树算法，根据树节点的分割点，将特征划分为不同的分箱区间，属于有监督的分箱方法。

   特征是否需要分箱是跟建模算法有关。风控评分卡模型需要很强的业务可解释性，所以在使用逻辑斯谛回归建模时，通常需要分箱处理；然而在使用 XGBoost、LightGBM 等机器学习算法时，通常是不需要分箱。

5. 类别特征离散化
   逻辑斯谛回归和支持向量机等算法要求所有特征是数值型变量，但在实际业务中会存在部分特征是类别型变量（例如性别、身份和职业等）。类别型变量可以分为两种：第一种是没有任何先后顺序或等级关系的标称类别变量（nominal category variable），例如性别、省份等；第二种则是有先后顺序或等级关系的有序类别型变量（ordinal category variable），例如学历、满意程度等。
   处理类别特征通常采用的方式是编码。编码分为两种：

• 一种是无监督编码方式，主要有序数编码和 one-hot 编码；

• 另一种则是有监督编码方式，主要有 Binary 编码、 Hashing 编码 、 CatBoost 编码等。
  当特征类别取值较多时，通常是先进行分箱，合并一些类别后再对分箱进行编码处理。
  无监督编码方式：

  • 序数编码
    序数编码（ordinal encoding）是一种简单的编码方式，直接对特征中的每个类别设置一个标号，将非数值特征转化为数值特征。一个有 N 种类别的特征可以与 [0, N-1] 中的整数一一对应。
    需要注意的是，序数编码只是将类别型变量更换了一种表达方式，其本质上还是离散的，数值化后的大小关系没有实际意义。
  • one-hot 编码
    one-hot 编码（one-hot encoding）也称“独热”编码，是指对每一种分类单独创建一个列，用 0 或 1 填充。
    
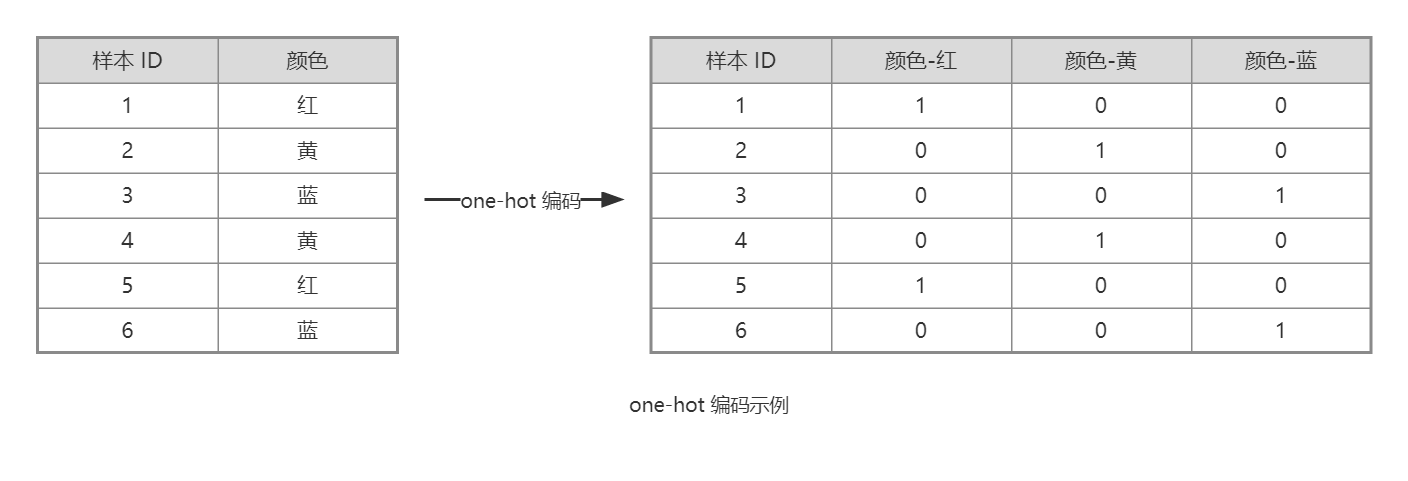
    需要注意的是，对于类别特别多的类别型变量，one-hot 编码会导致特征维度激增，特征更加稀疏，影响模型效果。

  有监督编码方式：

  • 目标编码
    目标编码（target encoding）也称均值编码，是一种有效表示类别型变量的方法。
    该方法将类别型变量的值映射为和标签 y 相关的统计指标，属于有监督编码方式。具体是将特征中的每个字替换为该类别的标签 y 的均值。但该方法严重依赖因变量的分布，会导致大大减少生成编码后特征的数量。
    • 在 分类模型 中，标签 y 的取值一般只有 0 和 1 两种，目标编码公式如下：

      X' = p(y=1 | X=Xtarget)

      计算特征值等于类别 Xtarget 时 y=1 的概率。
    • 在 回归模型 中，标签 y 是连续数值，目标编码公式如下：

      X' = sum(y | X=Xtarget) / sum(X=Xtarget)

      y | X=Xtarget 表示特征值等于类别 Xtarget 是 y 的取值。
  • WOE 编码
    WOE（Weight of Evidence，证据权重）是针对对原始特征的一种编码形式。
    WOE 编码（WOE encoding）适用于二分类问题的特征预处理。具体做法是使用特征中每种类别 y=1 的概率和 y=0 的概率的比值的对数替代每种类别的特征值。计算公式如下：

    WOEi = ln(p(Badi)/p(Goodi)) = ln((Badi/BadT)/(Goodi/GoodT)) = ln(Badi/BadT) - ln(Goodi/GoodT)

    其中 Badi 为类别 i 中标签为 1 的样本数，Goodi 为类别 i 中标签为 0 的样本数，BadT 为所有样本中标签为 1 的样本数，GoodT 为所有样本中标签为 0 的样本数。因此 WOE 可以表示“当前类别中坏样本占所有坏样本的比例”和“当前类别中好样本占所有好样本的比例”的差异。
    WOE 编码不仅可以处理类别特征，也可以处理连续特征。尤其是在评分卡模型中，使用逻辑斯谛回归算法拟合特征与逾期率的关系，首先会对连续特征进行分箱，然后利用各箱的 WOE 值代替特征值。

6. 特征交叉组合
   特征交叉组合是数据特征的一种处理方式，该方式可以增加特征的维度，组合的特征能够反映更多的非线性关系。
   实践中，通常会对类别特征进行组合；而对于连续特征，可以先进行分箱，再进行组合，也可以直接进行特征交叉衍生。

   • 离散特征分类组合
     对于类别型变量特征的交叉组合，特征 A 取值类别有 m 种，特征 B 取值类别有 n 种，可以通过笛卡尔积的方式进行特征组合，可以重新得到组合后的 m*n 个组合特征。
   • 连续特征交叉衍生
     特征交叉衍生的方式有很多种，常用的方式有：
     • 利用数值型特征之间的加、减、乘、除操作得到新特征；
     • 对已选定特征进行奇异值分解（SVD），将奇异值作为新特征；
     • 根据已选特征进行聚类，将所在类别的平均目标值或出现最多的值作为新特征，或者将所在类别与其他类别的距离作为新特征等；
     • 此外还可以利用深度学习技术衍生新特征，利用神经网络中某层的数据作为新特征也是一种思路。

   特征交叉组合会导致特征维度激增，组合后的特征因此可能会很稀疏，因此在实践中，需要根据特征含义组合出具有业务含义的特征。

特征选择

特征选择（feature selection）是指选择能够使模型获得最佳性能的特征子集。特征的必要性包括：

• 特征池中的特征并非都对模型有益，如果选取不稳定的的特征训练模型，那么最终生成的模型的稳定性较差。

• 线性模型要求特征间不能多重共线性，因此需要选择无严重共线性的特征建模。

• 选取尽可能对模型有增益的特征，剔除无用特征，从而降低特征维度缩短模型训练时间和减少对机器资源的损耗。

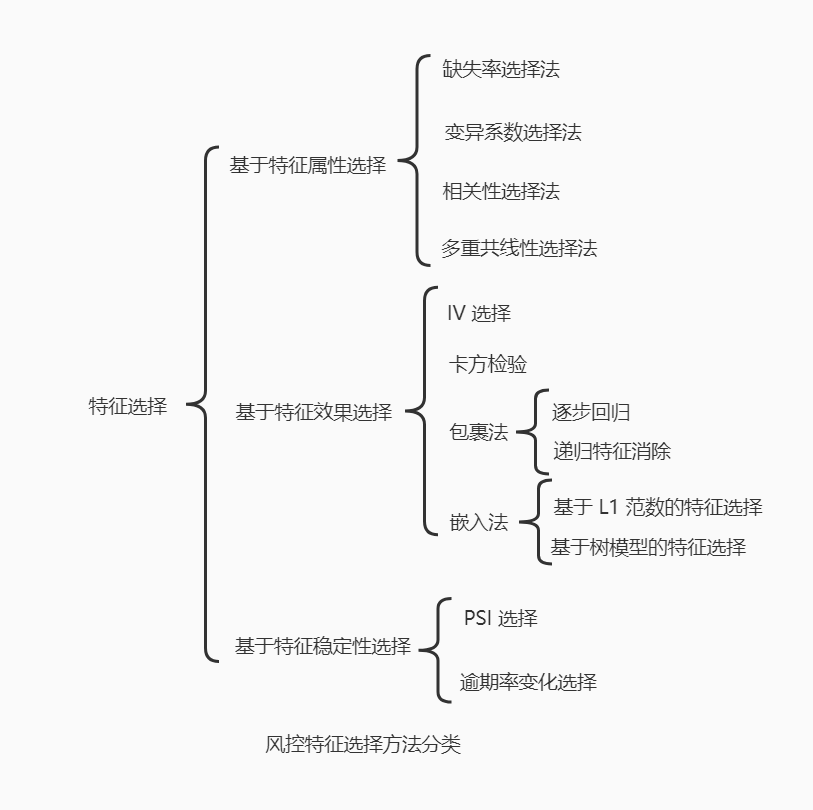
  特征选择一般都是反复迭代、验证，并且和模型训练过程循环进行，最终可以得到性能优异的模型。特征选择可以从基于特征属性选择、基于特征效果选择和基于特征稳定性三个方面。

基于特征属性选择

基于特征属性选择特征，不需要任何标签信息，直接根据特征值分布或特征之间的关系进行选择，计算速度快，一般用于特征初筛。主要方法有缺失率选择法、变异系数选择法、相关性选择法和多重共线性选择法。

1. 缺失率选择法
   一般情况下，当特征缺失率超过 95% 时就不再适合参与建模，首先要做的就是剔除特征。而当特征缺失率不超过 95% 时，可以采用缺失值处理方法进行处理。对于缺失率阈值，可以根据具体业务场景灵活调整。

2. 变异系数选择法
   变异系数（coefficient of variation）又称 离散系数 是概率分布离散程度的一个归一化量度，其定义为标准差与均值之比。
   变异系数反映了特征分布的离散程度，相比方差，变异系数是一个无量纲量，因此在比较两组量纲不同或均值不同的数据时，应该用变异系数而不是标准差。特征选择过程中会首先过滤变异系数为 0 的特征。
   如果某个特征的变异系数很小，则表示样本在这个特征上没有差异，可能特征中的大多数值都是一样的，甚至整个特征取值全部相同。

3. 相关性选择法
   相关性是衡量两个特征之间依赖关系的指标。度量特征相关性的指标有很多，常见的有以下三种：

   • Person 相关系数
     用来度量特征的 线性相关性，取值范围为 [-1, 1]，大于 0 表示两个特征正相关，小于 0 表示两个特征负相关，等于 0 则表示两个特征非线性相关。
   • Spearman 相关系数
     用来度量特征 单调相关性，取值范围为 [-1, 1]，大于 0 表示两个特征正相关，小于 0 表示两个特征负相关，等于 0 则表示两个特征非单调相关。
   • Kendall 相关系数
     用来度量特征 有序分类特征相关性，取值范围为 [-1, 1]，大于 0 表示两个特征正相关，小于 0 表示两个特征负相关，等于 0 则表示两个特征排名独立。

   逻辑斯谛回归等算法要求特征之间不得具有很强的相关性，否则会导致无法用特征系数解释最终模型的入模特征（即模型使用的特征）与目标变量之间的关系。

4. 多重共线性选择法
   多重共线性描述的是一个自变量与其他自变量（可以多个）之间的完全线性关系。方差膨胀系数（Variance Inflation Factor, VIF）是一种衡量共线性程度的常用指标，表示回归系数估计量的方差与假设特征间不线性相关时的方差的比值。
   VIF 计算公式如下：

   VIF = 1 / (1 - R^2)

   R^2 是某个特征对其余特征做回归分析的复相关系数。VIF 越大，该特征与其他特征的关系越复杂，多重共线性越严重。VIF < 10 则认为不存在多重共线性；10 <= VIF < 100 则认为存在较强的多重共线性；VIF >= 100 则认为存在严重的多重共线性。

基于特征效果选择

1. IV 选择
   IV（Information Value，信息价值）是衡量特征预测能力的关键指标。IV 和 WOE 之间的关系可以描述为：WOE 描述了特征和目标变量之间的关系；IV 用来衡量这种关系的强弱程度。
   WOE 分析特征各个分箱对于目标变量的预测能力，IV 用来反映特征的总体预测能力。IV 的计算公式即在第 i 箱 WOE 的基础上乘以系数，该系数表示该分箱坏样本比例和好样本比例的差。

   IV 范围	描述
   iv < 0.02	无预测能力，需放弃
   [0.02, 0.1)	较弱的预测能力
   [0.1, 0.3)	预测能力一般
   [0.3, 0.5)	预测能力较强
   iv > 0.5	预测能力极强，需检查

2. 卡方校验
   卡方校验是一种以卡方分布为基础的检验方法，主要用于类别变量，根据样本数据推断总体分布与期望分布是否有显著差异，或者推断两个类别变量是否相关或相互独立。其原假设为：观察频数与期望频数没有差别。

3. 包裹法

   • 逐步回归
     逐步回归（stepwise regression）是一种筛选并剔除引起多重共线性变量的方法，广泛应用于逻辑谛斯回归模型。
     其基本思想是将解释变量逐个引入模型，每引入一个解释变量都进行统计性假设检验，当原来引入的解释变量由于后来解释变量的引入变得不再显著时则将其删除，以确保每次引入新变量之前，回归方程中只包含显著性变量。
     逐步回归共有三种方式：

     • 前向逐步回归，将特征逐步加入。
     • 后向逐步回归，从所有特征集中将特征逐步剔除。
     • 双向逐步回归，前向加入与后向剔除同时进行，即在每次加入新特征的同时，将显著性水平低于阈值的特征剔除。

     一般情况下，双向逐步回归的效果比前向逐步回归和后向逐步回归好。

   • 递归特征消除
     递归特征消除（Recursive Feature Elimination, RFE）也是常用的包裹法特征选择方法，其基本思想是使用一个 基模型 进行多轮训练，每轮训练之后消除若干重要性低的特征（线性模型特征归一化后使用特征系数衡量其重要性），再基于特征集进行下一轮训练。

4. 嵌入法

   • 基于 L1 范数
     线性模型可以被看作是多项式模型，其中每一项的系数都可以表征这一维特征的重要性，越重要的特征在模型中对应的系数越大，而与输出变量相关性越小的特征，对应的系数越接近 0。
     L1 正则化将系数的 L1 范数作为 惩罚 项加到损失函数中，由于正则项非零，则会导致不重要的特征系数变为 0，因此使用 L1 正则化的模型往往稀疏，这使得 L1 正则化成为很好的特征选择方法。
     在使用线性模型进行 L1 正则化特征选择时，应先消除多重共线性。
   • 基于树模型
     建立树模型的过程就是特征选择。基于树模型的特征选择会根据信息增益或基尼不纯度的准则来选择特征进行建模，输出各个特征的重要度，依此进行特征筛选。

基于特征稳定性

1. PSI 选择
   PSI 指特征的稳定性指标，用于识别分布变化大的特征，充分了解其背后的特征分布变化的原因，判断是否可接受。其中稳定性是有参照的，在建模时将训练样本的分布作为预期分布（expected distributiopn），将 OOT 样本作为作为实际分布（actual distributiopn）。
   在计算 PSI 时需要先将特征值分箱。PSI 计算公式如下：

   PSI_i = (p(Actual_i) - p(Expected_i)) * ln(p(Actual_i)/p(Expected_i)) 
         = (Actual_i/Actual_t - Expected_i/Expected_t) * ln((Actual_i/Actual_t)/(Expected_i/Expected_t))

   其中 PSI_i 表示第 i 个分箱稳定性指标的结果，Actual_i 为第 i 个分箱实际样本个数，Expected_i 为第 i 个分箱期望样本个数，Actual_t 为实际样本总数，Expected_t 为期望样本总数。

   PSI 表示实际样本分布和期望样本分布的差异。

   PSI 范围	稳定性
   iv < 0.1	变化不太显著
   [0.1, 0.25]	有比较显著的变化
   iv > 0.25	变化剧烈，需要特殊关注

2. 逾期率变化选择
   在风控业务中，有些特征的不稳定性表现在对逾期率排序的衰减上，随着时间的变化特征对预测变量的排序会发生颠倒，称之为“倒箱”。
   PSI 反映的主要是特征分布的不稳定性，而“倒箱”体现特征对预测变量区分能力的不稳定性。

特征提取

特征提取（feature extraction）是指从原有较多的特征中计算出较少的特征，用新特征替换原有特征，达到降维的目的，即通过从样本中学习一个映射函数 f，将原特征矩阵 X1 映射到 X2，其中 X2 的维度小于 X1。
特征选择和特征提取都是为了特征降维，二者实现效果相同，当采用的方法不同。特征提取采用的是通过属性间的关系，如组合不同属性得到新属性以此改变原有的特征空间；特征选择采用的是从原始特征数据集中选用子集，这是一种包含关系并没有改变原始特征空间。
特征提取方法分为两大类：

• 线性特征提取方法
  • 主成分分析方法（Principal Component Analysis, PCA），映射后的样本具有更大的发散性。
  • 线性判别分析法（Linear Discriminant Analysis, LDA），映射后的样本具有较好的的分类性能。
• 非线性特征提取方法
  • 局部线性嵌入（Locally Linear Embedding, LLE），保持邻域内样本之间的线性关系。
  • 多维尺度变换（Multiple Dimensional Scaling, MDS），保持降维后的样本间距离不变。

线性特征提取

1. PCA
PCA 将高维的特征向量合并为低维的特征向量，是一种无监督的特征提取方法。其基本原理是通过线性投影，将高维数据映射到低维空间中表示，并且期望在所投影的维度上数据的方差最大（最大方差理论），以此使用较少的数据维度，留存较多的原始数据特性。
   PCA 是我们常用的特征提取方法，其优点如下：

   • 仅需要以方差衡量信息量，不受数据集以外的因素影响。
   • 各主成分之间正交，可消除原始数据成分间相互影响的因素。

   缺点如下：

   • 主成分各个特征维度的含义不如原始特征的解释性强。
   • 非主成分也可能含有重要信息，丢弃后会降低模型效果。

2. LDA
LDA 是一种基于分类模型进行特征属性合并的操作，是一种有监督的特征提取方法。其基本原理是将带有标签的数据投影到维度更低的空间中，使得投影后的点按类别区分，相同类别的点会在投影后的空间中更接近，用一句话概括就是：投影后相同类间方差最小，不同类间方差最大。
   LDA 的优点如下：

   • 在特征提取的过程中，可以使用类别的先验知识。
   • 在分类过程中，依赖均值而不是方差的时候，其优于 PCA 之类的算法。

   缺点如下：

   • 不适合对非高斯分布样本进行特征提取。
   • 可能过度拟合数据。

   除了 PCA 和 LDA 之外，线性特征提取方法还有因子分析（Factor Analysis, FA）、奇异值分解（Singular Value Decomposition, SVD）和独立成分分析（Independent Component Analysis, ICA）等。

非线性特征提取

1. LLE
LLE 是一种基于 流形学习 的方法（流形学习假设所处理的数据点分布在嵌入外围欧氏空间的一个潜在的流形体上，或者说这些数据点可以构成这样的一个潜在的流形体），其能够使特征提取后的数据较好地保存原有流形结构。LLE 假设数据在较小的局部是线性的，即每一个数据点都可以由其近邻点线性表示。
   LLE 主要分为三步，首先寻找每个样本点的 k 个近邻点；然后由每个样本点的近邻点计算出该样本点的权重；最后由该样本点的权重在低维空间中重构样本数据。至此就可以将特征映射到低维空间中。
   LLE 的优点如下：

   • 可以学习任意维度局部线性的低维流形。
   • 该方法归结为稀疏矩阵特征分解，计算复杂度较小且实现容易。

   缺点如下：

   • 学习的流形只能是不闭合的，且样本集是稠密、均匀的。
   • 该方法对最近邻接样本数的选择敏感，不同近邻数对最终结果有很大影响。

2. MDS
MDS 是将高维空间中的样本点投影到低维空间中，让样本彼此之间的距离尽可能不变。其基本原理是首先计算得到高维空间中样本之间的距离矩阵，接着计算得到低维空间的内积矩阵，然后对低维空间的内积矩阵进行特征值分解，并按照从大到小的顺序取前 d 个（d 表示低维空间的维度）特征值和特征向量，最后得到在 d 维空间中的距离矩阵。
   MDS 的优点如下：

   • 不需要先验知识，计算简单。
   • 保留样本在原始空间的相对关系，可视化效果较好。

   缺点如下：

   • 当有样本的先验知识时，他无法被充分利用，因此无法得到预期效果。
   • 该方法认为各维度对目标的贡献相同，忽略了维度间的差剧。

   除了 LLE 和 MDS 之后，非线性特征提取方法还有等度量映射（Isometric Feature Mapping, ISOMAP）和 t-SNE 等。

训练、概率转化和效果评估

特征选择和特征提取之后就是关键的模型训练环节，首先模型训练基础知识，其次概率转化方法，最后评价模型效果以及选择合适的模型。

模型训练

机器学习的模型训练其本质是参数优化过程。其参数可以分为两种：一种是模型参数（parameter）；另一种是超参数（typerparameter）。
模型参数是可以直接通过数据估计得到的，如线性回归模型中的回归参数。超参数是用来定义模型结构或优化策略的，通常需要在模型训练前根据经验给定，如正则化系数。因此模型训练的目标是找到使得最终模型最好的超参数组合。

模型调参是寻找最优超参数组合的过程。常见的模型调参方法有以下几种：网格搜索（grid search）；随机搜索（random search）；贝叶斯优化（bayesian optimization）。

交叉验证的方法有以下几种：

• 留 p 法交叉验证。
• 留一法交叉验证。
• K 折交叉验证。

概率转化

风控模型（如 XGBoost 模型、LighrGBM 模型、LR （逻辑斯谛回归）模型）直接输出的是客户逾期概率，在风控信贷场景中，需要将概率转化为评分，通过分数量化客户的风险等级。
转换为评分的额方法如下：设 p 为客户逾期概率，那么客户逾期概率与未逾期概率的比值 p/(1-p) 记为 oods。转换为评分的计算公式如下：

score = A - B * log(odds) = A - B * log(p / 1-p)

客户逾期概率越低，评分越高。在通常情况下，这是分值的变动方式，即高分值代表低风险，而低分子代表高风险。其中 A 和 B 都是常数，在计算时通常需要做出两个假设：给定 odds = Ratio 时，预期分数为 Base；odds 翻倍时，分数减少值为 PDO(Point of Double Odds)。由此可以得到 A = Base + B * log(2 * Ratio), B = PDO / log2。

模型效果评估

根据模型对样本的预测分数和样本的真实标签，可以通过不同角度的指标来评估模型的效果。
通过多种指标对模型性能进行评价，不同的评价指标往往产生不同的评价效果，这表明模型的 好坏 是相对的，具体使用何种指标取决于实际使用场景。
样本根据其真实类别和模型预测类别可形成以下四种组合：

• 真正例（True Positive, TP）：真实类别为正例，预测类别为正例。
• 假正例（False Positive, FP）：真实类别为负例，预测类别为正例。
• 假负例（False Negative, FN）：真实类别为正例，预测类别为负例。
• 真负例（True Negative, TN）：真实类别为负例，预测类别为负例。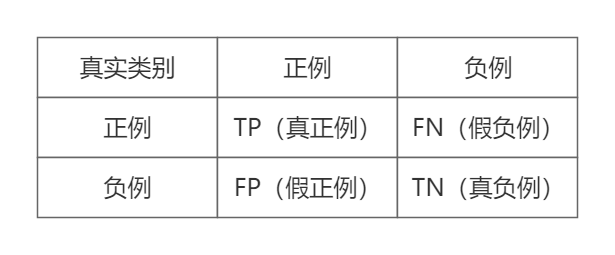
  

对于回归任务，常见的评价指标有 RMSE（平方根误差）、MAE（平均绝对误差）、MSE（平均平方误差）和 coefficient of determination（决定系数）。对于分类任务，常见的评价指标有准确率、精确率、召回率、F1 值、AUC 和 KS 等。

• 准确率
  准确率（accuracy）是指正确预测的正负例样本数和总样本数的比值。accuracy = (TP + TN) / (TP + FP + FN + TN)。
• 精确率
  准确率（precision）又称查准率，是指预测为正例的样本中真正是正例的样本比例。precision = TP / (TP + FP)。
• 召回率
  召回率（recall）又称查全率，是指实际正例样本中模型预测为正例的样本比例。recall = TP / (TP + FN)。
• F1 值
  F1 值是精确率和召回率的调和值，更接近于两个数中较小的那个，因此精确率和召回率接近时，F1 值更大。F1 = (2 * precision * recall) / (precision + recall)。
• AUC
AUC(Area Under Curve) 为 ROC 曲线下的面积。ROC(Receiver Operating Characterstic, 接收者工作特征) 曲线源于雷达信号分析技术，ROC 曲线的横坐标为 FPR（假正率），FPR = FP / (FP + TN)，即被预测为正例的负样本数与真实负样本数的比值；纵坐标为 TPR（真正率），TPR = TP / (TP + FN)，即被预测为正例的正样本数与实际正样本数的比值。AUC 的取值范围为 0~1。
• KS
KS（Kolmogorov-Smirnov） 指标主要用来验证模型对客户 好坏 的区分能力，用以检验两个经验分布是否不同，或者一个经验分布与一个理想分布是否不同。
  在计算风控模型 KS 指标时，通常是在模型对样本打分后，对分数进行分箱，然后分别统计每箱累积 好 客户和累积 坏 客户与 好 客户和 坏 客户总体的比值，累计 坏 客户比例与累计 好 客户比例的差值即为每箱对应的 KS 值。
  模型 KS 定义为各分箱 KS 值得最大值：KS = max(Pcum(Bad) - Pcum(Good))，KS 值越高，模型越好。但过高的 KS 值可能意味者过度拟合或特征 穿越 等。
  相比 KS，AUC 更加稳健。而相比准确率、召回率、F1 值等指标，AUC 指标优势在于不需要设定分类阈值，只需要关注预测概率的排序，因此一般在二分类模型中主要将 AUC 作为模型效果的评价指标。

---

开发方法论-上线和维护

模型训练通常在本地环境中进行，训练完成后，首先选择最优模型并部署到线上环境，然后验证模型在线上环节运行是否准确无误，确认无误后，才会使用。

部署及上线验证

1. 模型部署
   模型部署是将训练完成的模型部署到线上环境。考虑其是否可以跨语言部署，模型文件通常可以选择保存为以下两种方式：

• pickle 格式
  pickle 是 Python 语言独有的格式。若线上为 Python 环境，那么就可以通过 pickle 格式实现模型的快速读取。

  # 使用 pickle 格式保存和读取模型
  def save_model_as_pkl(model, path):
  	import pickle
  	with open(path, 'wb') as f:
  		pickle.dump(model, f, protocol=2)
  
  def load_model_from_pkl(path):
  	import pickle
  	with open(path, 'rb') as f:
  		model = pickle.load(f)
  	return model

  保存模型时设置 protocol=2 ，表示以二进制协议对模型内容进行序列化存储，以此解决 Python3 环境中保存的模型在 Python2 环境中部署。
• PMML 格式
  预测模型标记语言（Predictive Model Markup Language, PMML）是一套与平台和环境无关的模型标记语言，可实现跨平台的机器学习模型部署。

2. 上线验证
   模型部署到线上环境后，通常先作为空跑一段时间使用，当积累一定样本量时可以进行上线验证。上线验证的目的在于确认模型在线上环境中按照预期运行。验证方式主要有以下三种：预测分数的一致性；模型分分布的差异性；模型效果的一致性。

监控和异常处理

模型上线之后，为了保证模型有效运行，需要对模型相关指标进行监控。当遇到异常状况时，可以通过多种途径发出预警。

模型监控

模型监控主要以报表方式展示各项监控指标。

• 模型监控内容
  模型监控包含准确性、稳定性和有效性三个方面。
  • 准确性是模型有效运行的基础。模型打分准确性监控是要确保线上模型的结果与线下模型计算的结果一致。
  • 稳定性是模型有效运行的保障。稳定性监控主要是监测模型分和特征是否稳定，可以从以下两个方面来判断：模型分布变化；特征值的分布变化。
  • 有效性是模型运行的目标。模型有效性监控是指持续监控模型的预测能力，识别其是否有衰减。监控指标主要依赖于 KS 和 AUC 指标，以及特征的 IV 指标。
• 模型监控形式
  模型监控可以按照日报、周报和月报形式，采用邮件或可视化页面的方式展示监控结果。

模型预警

模型预警主要是根据预警条件触发预警信息，提示模型异常，因此需要定义预警指标触发条件和预警形式。
对每一项监控设定预警指标并定义预警阈值，当监控的指标值偏离该范围时就会发出预警。对应模型的准确性、稳定性和有效性监控，预警指标有一致性、 PSI 和 KS ，然后进一步根据指标的风险程度划分预警等级。
预警指标阈值没有统一的设置规范，不同业务场景对风险的容忍度有所差别，因此需要结合具体场景和业务相关人员共同确定阈值。

异常处理

模型异常处理是指模型发生异常时，需要快速分析问题和解决问题，将影响尽可能降到最低。导致模型的准确性、稳定性和有效性异常的原因有很多，下面为常见的原因：

• 模型准确性异常处理
  导致模型准确性异常的原因通常有以下两种：运行环境发生改变；特征预处理逻辑发生改变。
• 模型稳定性异常处理
  导致模型稳定性异常的原因通常有以下两种：数据源异常；客群变化。
• 模型有效性异常处理
  导致模型有效性异常的原因通常有：数据源异常；客群变化；模型自身效果衰减。

迭代优化

模型上线之后，客群的变化、数据维度的增加、业务调整某些数据无法使用等都可能导致模型效果出现波动。面对这些情况对模型的迭代和优化就显得格外重要，当然模型迭代优化的目的在于提升线上模型效果，使得模型在近期样本上表现更好。
模型的迭代优化可以从模型融合、建模时效和拒绝推断三个方面进行。

模型融合

模型融合角度优化是指将多个模型的结果相互组合或再训练，以提升最终模型效果。
不同样本之间的信息千差万别，不同算法从样本中学到的信息也各不相同，因此可以利用这些差异结合不同类型、不同时间段模型相互融合，提炼出更加丰富的客群信息。融合模型突破了以往单一模型的局限性，具有多个子模型的优点，比单一模型具有更好的效果。

1. 模型融合方法
   模型融合的方法有很多种，常用的有以下三种：

   • 模型结果简单加权是指直接给各个子模型分配权重，通过加权求和得到融合模型的输出。
   • 模型结果再训练是指将各个子模型的结果作为特征，采用机器学习算法再次建模，最终得到融合模型。
   • 集成学习通过构建多个学习器来完成建模任务。集成学习中常用的四种模型融合方法：
     • Bagging 是在多轮采样获取的数据子集上训练多个个体学习器，然后通过投票法或平均法对个体学习其进行集成的方法。
     • Boosting 是一种在训练过程中，不断对训练样本分布进行调整，基于调整后的样本分布训练下一轮个体学习器的集成学习方法。
     • Stacking 是一种将多种个体学习器整合在一起来取得更好表现的集成学习方法。一般情况下，Stacking 的训练过程分为两步，第一步训练第一层的多个不同模型，第二部以第一层各个模型的输出来训练得到最终模型。
     • Blending 与 Stacking 类似，区别体现在于：第一步在训练集上，Blending 不是通过 K 折交叉验证策略得到预测值，而是采用 Hold-Out 策略，即保留固定比例的样本并将其作为验证集，在其余样本上训练出多个模型，分别在验证集和测试集上进行预测，将预测值作为新特征；第二步基于验证集和测试集的新特征，训练得到最终模型。

2. 模型融合方式
   模型融合方式有很多，包括不同标签模型融合、不同样本模型融合和不同数据源模型融合。

   • 不同标签模型融合是指将不同样本标签开发模型继续宁融合。基于不同样本标签，模型能够学到样本不同维度的信息，融合后的模型学到的信息更加丰富。
   • 不同样本模型融合是指将不同样本开发的模型进行融合。根据产品、时间等信息，将样本分群，分别训练子模型，再将子模型融合。
   • 不同数据源模型融合是指先根据不同数据源特征分别建立子模型，再将不同数据源子模型融合。

建模时效

从建模时效角度优化是指快速迭代模型，及时根据线上客群变化做出调整。因为通常情况下在模型上线后，模型更新周期会较长，不能快速反映客群变化，即使发现了线上模型效果衰减，再次开发新的模型也需要一段时间。为此解决建模时效问题的常见做法是应用模型自动快速迭代和在线学习。

1. 模型自动快速迭代
   模型自动快速迭代是指加入最新有表现样本，快速更新迭代模型。
   核心部分主要包含样本选择、数据准备、数据预处理、特征选择、模型训练和效果评估。为此可以构建一套完整的模型自动化平台，将样本选择、数据准备、自动测试和部署上线也实现自动化，这样就构建了完整的模型自动快速迭代体系。该模型自动快速迭代体系主要包括 特征自动回溯系统、自动建模系统、自动测试系统 和 自动上线系统 四个部分。

2. 在线学习
   在线学习（online learning）是指根据线上的实时数据，快速进行模型调整，使得模型及时反映线上的变化，提高线上模型的效果。
   在线学习种具有代表性的算法： Bayesian Online Learning 和 Follow The Regularized Leader(FTRL) 。
   传统模型开发是使用离线数据处理方式进行开发的，开发完成后再部署到线上，这种模型上线后一般是静态的，不会与线上的业务数据有任何互动。
   相比模型自动快速迭代，在线学习方法不需要每次使用全量样本重建模型，只需要使用新增样本更新模型参数，建模成本低。

拒绝推断

拒绝推断通常是基于放款样本，但贷前风险预测模型使用场景是所有的授信申请客户，其中包含拒绝样本，即训练模型使用的客群仅是预测人群中的一部分，存在“样本偏差”问题。如果能在建模样本中加入被拒绝的样本，那么模型的效果可以得到保障，但是问题在于，被拒绝的样本没有标签，而推测被拒绝样本的标签就是 “拒绝推断” 的主要内容。

1. 使用场景
   拒绝推断经常使用的场景：总体风险异质；风险通过率很低；历史数据与当前数据显著不同。
   已知推断比（known-to-inferred odds ratio, KI）常用来衡量拒绝推断的风险是否合理，定义式如下：

   KI = (Gk/Bk)/(Gi/Bi)

   其中 Gk、Bk、Gi、Bi 分别表示已知好客户、已知不良客户、推断好客户、推断不良客户的样本数量。KI 值越高，说明推断人群中不良客户的比例越高，推断人群的风险也就越高。通常合理的 KI 值在 2 ~ 4 之间，而业界倾向于更大的值。

   拒绝推断场景中常见的三种模型如下：

   • AR(Accept Reject) 模型：以是否放贷为标签，是在全量样本上构建的模型。
   • KGB(known Good Bad) 模型：以逾期表现为标签，是在已知好坏标签的样本上构建的模型。
   • AGB(All Good Bad) 模型：以逾期表现为标签，是在全部授信申请样本上构建的模型。建模样本包含已知好坏标签（真实标签）的样本和推断出“伪标签”的样本。

2. 常用方法
   解决样本偏差问题的方法有两类：

   • 数据法
     • 增量下探法
       增量下探法是指从本该拒绝的样本中，随机选取部分样本授信通过，以便获取该部分样本的真实标签。
     • 同生表现法
       同生表现法是指通过客户在其他产品或机构的贷后表现，推断出本产品上的伪标签。
   • 推断法
     • 硬截断法
       硬截断法（hard cutoff）也称简单展开法（simple augmentation），是指根据通过样本构建 KGB 模型，利用 KGB 模型对拒绝样本预测打分，设置截断阈值，高于该阈值的样本认定为正样本，低于该阈值的样本认定为负样本，最终将有真实标签的通过样本和推测得到的伪标签的拒绝样本合并，构建最终模型。
     • 模糊展开法
       模糊展开法（fuzzy augmentation）是指根据通过样本构建 KGB 模型，利用 KGB 模型预测拒绝样本的逾期概率，然后将每条拒绝样本复制为不同类别、不同权重的两条，每条通过样本的权重为 1，最终将有真实标签的通过样本和推断得到伪标签的决绝样本合并，考虑不同样本的权重，构建最终模型。
     • 重新加权法
       重新加权法（reweighting）是指根据通过样本构建 KGB 模型，利用 KGB 模型对全部样本预测打分，然后分箱统计不同分数段的通过样本数和拒绝样本数，计算每箱的权重，添加通过样本不同分数段的权重，然后利用通过样本构建最终模型。
       权重方式计算如下：

       weight = (Accepti + Rejecti) / Accepti

       其中 Accepti 表示第 i 分箱通过样本数，Rejecti 表示第 i 分箱拒绝样本数。
     • 外推法
       外推法（extrapolation）是指根据通过样本构建 KGB 模型，利用 KGB 模型对拒绝样本预测打分，然后对通过样本模型分等频分箱，统计每箱的逾期率，将逾期率的 KI 倍数设为拒绝样本相同分箱的期望逾期率，并按照期望逾期率对拒绝样本随机标记伪标签，最终和通过样本一起构建最终模型。
     • 迭代再分类法
       迭代再分类法（iterative reclassification）是指通过多次迭代，使得最终模型参数逐步趋于稳定。迭代再分类的具体做法：首先利用硬截断法获得拒绝样本的伪标签，然后训练得到最终模型，并利用最终模型重新给拒绝样本预测打分，更新伪标签，直到任何一个有价值的指标收敛。
       迭代再分类法利用启发式思想，经过多次迭代，可以保证修正偏差后的最终模型的效果。其中设置的迭代终止条件可以是任何一个有价值的指标收敛。
     • 双变量推断法
       双变量推断法（bivariate inference）是指首先分别利用通过样本构建 KGB 模型和全部样本构建 AR 模型，然后利用两个模型分别对拒绝样本预测打分，并将加权求和的结果作为最终预测打分，然后利用 “外推法” 设置伪标签，最终和通过样本一起构建模型。
       拒绝样本的模型分计算公式如下：

       Rejects = a * ARs + (1-a) * KGBs

       其中 ARs 是 AR 模型的打分，KGBs 是 KGB 模型的打分，0 < a < 1 表示权重。

---

常见风控建模算法

风控建模可用的算法有很多种，但是所有算法遵循的原则都是类似的，即从数据中提取一种无限接近于数据内部真实联系的映射关系。换言之就是给定特征集 x 和标签 y，存在某种未知的映射关系 f，使得 x 和 y 能够一一对应，即 y = f(x)。抽象出来映射关系 f 是数据内部存在的真实联系。
预测结果 h(x) 和标签 y 之间的误差用损失函数来衡量。其中损失函数、代价函数和目标函数是三个非常容易混淆的概念，其含义分别如下：

• 损失函数（loss function）：定义在单个样本上，是指一个样本的误差。
• 代价函数（cost function）：定义在整个训练集上，是指所有样本误差的平均，也就是所有损失函数值的平均。
• 目标函数（object function）：是指最终需要优化的函数，一般来说在代价函数的基础上，增加了正则项。

各种算法通过构造不同的假设空间定义目标函数，通过优化目标函数在假设空间中寻找最优的映射关系 h，其本质还是最优化问题。

这里对下面的算法不会有太深的研究，有兴趣的可以自行学习。

基础学习算法

1. 逻辑斯谛回归

2. 支持向量机

3. 决策树

集成学习算法

1. 随机森林

2. GBDT

3. XGBoost

4. LightGBM

深度学习算法

1. 深度神经网络

2. 卷积神经网络

---

模型体系搭建

信贷产品生命周期主要包括营销、贷前、贷中和贷后四个阶段，每个阶段都有风险控制的需求。

• 贷前阶段主要获取并筛选客户流量，以营销响应模型和流量筛选模型为主。
• 贷前阶段一般会通过部署多种风控规则和模型来识别风险，风控规则可以识别小部分高风险客户，大部分仍然需要模型预测。贷前阶段的模型主要有反欺诈模型、信用风险模型。
• 贷中阶段会通过贷中行为预测客户的风险情况，制订账户管理等策略，同时利用交易风险模型对客户贷中的提现、消费等交易行为进行风险判断。
• 贷后阶段通过还款预估模型预测客户的还款可能性，制订合理的催收策略，提升还款率；利用失联预估模型预测客户的失联概率，优化催收策略。

完整的风控体系需要对信贷产品生命周期的每一个阶段进行有效的风险控制，以下为信贷产品生命周期的不同阶段包含的主要风控模型。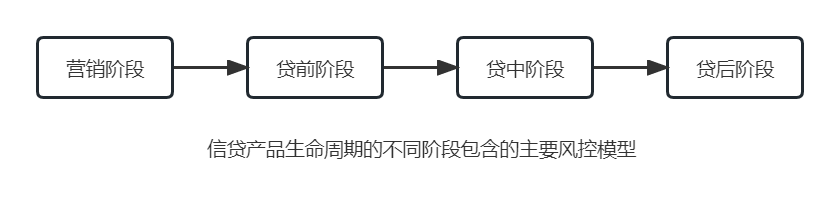

营销阶段

营销是业务开展的第一步，获取优质客群是营销阶段得到重要目标，通常是利用营销响应模型评估客户的响应概率，再利用流量筛选模型选择目标客群。

1. 营销响应模型
   营销响应模型是通过营销时对客户进行评估来预测客户响应概率的模型。营销场景主要包含纯新客户名单营销、流失客户营销召回和存量客户的交叉销售等，采用营销响应模型将客户分级，对于响应概率高的客群，业务人员可以重点营销，即可以大幅提升营销效率，降低营销成本。

2. 流量筛选模型
   流量筛选模型也称前筛模型，用来识别资质明显差的客群。拦截这部分高风险客群是风险控制的第一项任务同时节省后续申请授信环节的数据成本。其中流量筛选模型一般用于与其他流量提供方合作的场景中。

贷前阶段

贷前是有效控制风险的重要阶段，因为一旦高风险客户通过贷前授信，后期在贷中和贷后阶段会面临被动局面，因此贷前阶段一般通过部署多种模型来尽可能多识别风险。

1. 反欺诈模型
   反欺诈模型用于识别欺诈风险高的客户。常见的欺诈类型有：第一方欺诈，即利用不实信息欺诈，欺诈者故意提供虚假申请信息以获得授信审批；第三方欺诈，即冒用他人身份欺诈，欺诈者偷取他人信息，以他人名义申请。
   因此在实践中可通过身份验证、活体识别和第三方数据验证等方式识别欺诈，并且可以通过反欺诈模型综合多维度信息进行识别。

2. 信用风险模型
   信用风险模型是通过对信贷申请人的信用状况进行评估来预测其未来逾期概率的模型，即申请评分卡，也称 A 卡（Application scorecard）。信用风险模型有重要作用，该模型的预测评分不仅可以审批准入，还可以用于额度和费率的设定。

贷中阶段

贷中阶段可以获得客户交易、还款和 APP 使用等行为数据，通过这些数据可以全面、客观、准确地预测客户的未来表现，从而制订有针对性的贷中管理策略。

1. 贷中行为模型
   贷中行为模型即行为评分卡，也称 B 卡（Behavior scorecard）是根据客户借款后的行为表现，预测其未来逾期概率的模型。

2. 交易风险模型
   交易行为模型是在已经获得授信的客户发生支用或消费交易等行为时进行风险预估的模型。该模型用于拦截高风险交易，及时止损，交易风险模型与信用风险模型类似，只是交易风险模型在获得的特征维度上会包含更多的贷中行为数据。

贷后阶段

贷后阶段的模型根据客户放贷后的行为表现，预测客户的还款概率。原始催收表现为尽可能多地联系客户，然后依靠客户近期的逾期行为调整策略。

1. 还款预估模型
   还款预估模型即催收评分卡，也称 C 卡（Collection scorecard）是预测已逾期的客户在未来一段时间的还款概率的模型。通常逾期客户在早期还款的可能性较大，越往后还款越困难，因此可以利用还款预估模型制订差异化的催收策略，提高还款率。

2. 失联预估模型
   失联预估模型预测已逾期的借款人在未来一段时间是否会失联。在催收后期，通常会出现无法联系到客户的情况出现，这对催收有很大的影响，如果可以在早期获得客户失联的可能性，即可以对催收工作的开展提供指导。

---

术语介绍

1. 样本、特征、标签
   样本是构建机器学习模型时需要一个数据集。
   特征是用来表征关注对象的特点或属性的一系列数据。
   标签是机器学习模型将要学习和预测的目标。

2. 账龄
   账龄（Month on Book, MOB）是指多期信贷产品从首次放款起所经历的月数。
   通常使用 MOBn 表示账龄，以月末时间点来看放款日经历 n 个完整的月数，具体如下：

   • MOB0：放款日到当月月底，观察时间点为放款当月月末。
   • MOB1：放款后第二个月，观察时间点为放款第二个月月末。
   • 以此类推 MOB 的最大值取决于信贷产品的 账期。

3. 逾期
   逾期的概念有以下几种：

   • 逾期天数（Days Past Due, DPD）：实际还款日与应还款日的相差天数。
   • 首期逾期天数（First Payment Deliquency, FPD）：分期产品中第一期实际还款日与应还款日的相差天数。
   • 逾期期数：贷款产品中客户的逾期期数，也指将逾期期数按区间划分后的逾期状态。
     通常以 30 天为区间划分，英文字母 M 来表示，具体如下：
     • M0：当前未逾期。
     • M1：逾期一期，或逾期 1~30 天。
     • M2：逾期两期，或逾期 31~60 天。
     • 以此类推，M2+ 表示逾期两期以上，或逾期天数未 61 天以上，和 DPD60+ 含义一致。
   • 逾期率：分为订单逾期率和金额逾期率。订单逾期率是指逾期订单数与总放款订单数的比值。金额逾期率是指逾期金额与总放款金额的比值。

---

引用

---

个人备注

此博客内容均为作者学习所做笔记，侵删！
若转作其他用途，请注明来源！